题目内容
一名工人要看管三台机床,在一小时内机床不需要工人照顾的概率对于第一台是0.9,第二台是0.8,第三台是0.85,求在一小时的过程中不需要工人照顾的机床的台数X的数学期望(均值).
2.55台
先确定X的所有可能的值为0,1,2,3,然后然后由独立事件和互斥事件的概率公式求出对应的每个值的概率.再根据期望公式求出所求的值.
解:由题意,可知X的所有可能的值为0,1,2,3,记事件A为第一台机床不需照顾;事件B为第二台机床不需照顾,事件C为第三台机床不需照顾,由独立事件和互斥事件的概率公式可知,P(X=0)=P(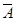 ·
·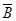 ·
·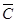 )=P(
)=P(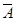 )P(
)P(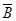 )P(
)P(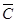 )=0.1×0.2×0.15=0.003,
)=0.1×0.2×0.15=0.003,
P(X=1)=P(A·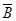 ·
·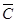 +
+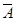 ·B·
·B·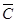 +
+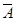 ·
·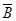 ·C)=P(A)P(
·C)=P(A)P(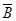 )P(
)P(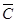 )+P(
)+P(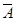 )P(B)P(
)P(B)P(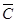 )+P(
)+P(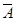 )P(
)P(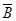 )P(C)=0.056,
)P(C)=0.056,
同上可得P(X=2)=0.329,P(X=3)=0.612,
所以E(X)=0×0.003+1×0.056+2×0.329+3×0.612=2.55台.
解:由题意,可知X的所有可能的值为0,1,2,3,记事件A为第一台机床不需照顾;事件B为第二台机床不需照顾,事件C为第三台机床不需照顾,由独立事件和互斥事件的概率公式可知,P(X=0)=P(
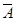 ·
·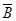 ·
·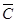 )=P(
)=P(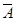 )P(
)P(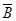 )P(
)P(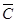 )=0.1×0.2×0.15=0.003,
)=0.1×0.2×0.15=0.003,P(X=1)=P(A·
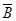 ·
·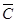 +
+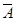 ·B·
·B·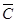 +
+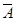 ·
·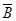 ·C)=P(A)P(
·C)=P(A)P(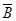 )P(
)P(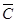 )+P(
)+P(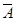 )P(B)P(
)P(B)P(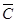 )+P(
)+P(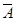 )P(
)P(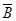 )P(C)=0.056,
)P(C)=0.056,同上可得P(X=2)=0.329,P(X=3)=0.612,
所以E(X)=0×0.003+1×0.056+2×0.329+3×0.612=2.55台.

练习册系列答案
相关题目
 服从二项分布
服从二项分布 ,且
,且 则
则 等于( )
等于( )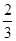

 上取一点P,使△PBC的面积大于
上取一点P,使△PBC的面积大于 的概率是____________
的概率是____________ 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为 。
。 ,求
,求 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:


















 ,则
,则 的值为( )
的值为( ) 



 =(m,n),
=(m,n), =(3,6),则向量
=(3,6),则向量