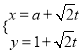题目内容
【题目】已知f(x)=9x﹣2×3x+4,x∈[﹣1,2].
(1)设t=3x , x∈[﹣1,2],求t的最大值与最小值;
(2)求f(x)的最大值与最小值.
【答案】
(1)解:设t=3x,∵x∈[﹣1,2],函数t=3x 在[﹣1,2]上是增函数,故有 ![]() ≤t≤9,故t的最大值为9,t的最小值为
≤t≤9,故t的最大值为9,t的最小值为 ![]()
(2)解:由f(x)=9x﹣2×3x+4=t2﹣2t+4=(t﹣1)2+3,可得此二次函数的对称轴为 t=1,且 ![]() ≤t≤9,
≤t≤9,
故当t=1时,函数f(x)有最小值为3,
当t=9时,函数f(x)有最大值为 67
【解析】(1)设t=3x , 由 x∈[﹣1,2],且函数t=3x 在[﹣1,2]上是增函数,故有 ![]() ≤t≤9,由此求得t的最大值和最小值.(2)由f(x)=t2﹣2t+4=(t﹣1)2+3,可得此二次函数的对称轴为 t=1,且
≤t≤9,由此求得t的最大值和最小值.(2)由f(x)=t2﹣2t+4=(t﹣1)2+3,可得此二次函数的对称轴为 t=1,且 ![]() ≤t≤9,由此求得f(x)的最大值与最小值.
≤t≤9,由此求得f(x)的最大值与最小值.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.