题目内容
(2007•烟台三模)在正三棱锥A-BCD中,E、F分别为棱AB、CD的中点,设EF与AC所成角为α,EF与BD所成角为β,则α+β等于( )
分析:取AD的中点G,连结EG、FG,取BD的中点H,连结AH、CH.由线面垂直的判定与性质,证出BD⊥AC.由三角形中位线定理,得到∠EGF就是异面直线AC、BD所成的角,即∠EGF=
.且∠EFG和∠FEG分别等于EF与ACBD所成角,由此在Rt△EFG中算出∠EFG+∠FEG=
,即得得α+β的值.
| π |
| 2 |
| π |
| 2 |
解答:解:取AD的中点G,连结EG、FG,取BD的中点H,连结AH、CH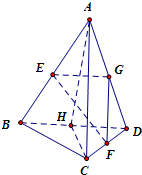
∵AD是等腰△ABD与等腰△BCD公共的底面,H为BD中点
∴AH⊥BD且CH⊥BD
∵AH、CH是平面ACH内的相交直线
∴BD⊥平面ACH,可得BD⊥AC
∵EG是△ABD的中位线,
∴EG∥BD,同理可得FG∥AC
因此,得到∠EGF就是异面直线AC、BD所成的角,即∠EGF=
∵EF与AC所成角为α=∠EFG,EF与BD所成角为β=∠FEG
∴Rt△EFG中,∠EFG+∠FEG=
,可得α+β=
故选:D

∵AD是等腰△ABD与等腰△BCD公共的底面,H为BD中点
∴AH⊥BD且CH⊥BD
∵AH、CH是平面ACH内的相交直线
∴BD⊥平面ACH,可得BD⊥AC
∵EG是△ABD的中位线,
∴EG∥BD,同理可得FG∥AC
因此,得到∠EGF就是异面直线AC、BD所成的角,即∠EGF=
| π |
| 2 |
∵EF与AC所成角为α=∠EFG,EF与BD所成角为β=∠FEG
∴Rt△EFG中,∠EFG+∠FEG=
| π |
| 2 |
| π |
| 2 |
故选:D
点评:本题在三棱锥中求异面直线所成的角,着重考查了正棱锥的性质、线面垂直的判定与性质和异面直线所成角的求法等知识,属于中档题.

练习册系列答案
相关题目
 (2007•烟台三模)一个多面体的直观图(正视图、侧视图,俯视图)如图所示,M,N分别为A1B,B1C1的中点.
(2007•烟台三模)一个多面体的直观图(正视图、侧视图,俯视图)如图所示,M,N分别为A1B,B1C1的中点.