Question

【题目】销售甲、乙两种商品所得利润分别是y1 ， y2万元，它们与投入资金x万元的关系分别为y1=m +a，y2=bx，（其中m，a，b都为常数），函数y1 ， y2对应的曲线C1 ， C2如图所示．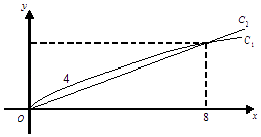

（1）求函数y1与y2的解析式；
（2）若该商场一共投资10万元经销甲、乙两种商品，求该商场所获利润的最大值．

Answer 1

【答案】
（1）解：由题意 ，解得m=2，a=﹣2，

又由题意8b=4得 ， ，（x≥0）

（2）解：设销售甲商品投入资金x万元，则乙投入（10﹣x）万元

由（1）得

令 ，则有x=t2﹣1，

，

当t=2即x=3时，y取最大值

答：该商场所获利润的最大值为 万元

【解析】（1）根据所给的图象知，列出关于m，a的方程组 ，解出m，a的值，即可得到函数y1、y2的解析式；（2）对甲种商品投资x（万元），对乙种商品投资（10﹣x）（万元），根据公式可得甲、乙两种商品的总利润y（万元）关于x的函数表达式；再利用配方法确定函数的对称轴，结合函数的定义域，即可求得总利润y的最大值．