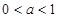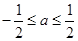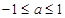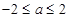题目内容
已知:函数f(x)=x -bx+3,且f(0)=f(4)。
-bx+3,且f(0)=f(4)。
(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;
(2)求函数y=f(x)在区间[0,3]上的最大值和最小值。
 -bx+3,且f(0)=f(4)。
-bx+3,且f(0)=f(4)。(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;
(2)求函数y=f(x)在区间[0,3]上的最大值和最小值。
解:(1)由f(0)=f(4),得b=4, 2分
所以,f(x)=x -4x+3,函数的零点为1,3, 4分
-4x+3,函数的零点为1,3, 4分
依函数图象,所求集合为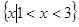 。 6分
。 6分
(2)由于函数f(x)的对称轴为x=2,开口向上,
所以,f(x)的最小值为f(2)=-1, 8分
f(x)的最大值为f(0)=3 10分
所以,f(x)=x
 -4x+3,函数的零点为1,3, 4分
-4x+3,函数的零点为1,3, 4分依函数图象,所求集合为
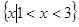 。 6分
。 6分(2)由于函数f(x)的对称轴为x=2,开口向上,
所以,f(x)的最小值为f(2)=-1, 8分
f(x)的最大值为f(0)=3 10分
略

练习册系列答案
相关题目
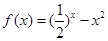 的零点个数是____
的零点个数是____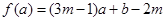 ,当
,当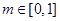 时,
时,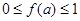 恒成立, 则
恒成立, 则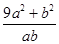 的最大值与最小值之和为( )
的最大值与最小值之和为( )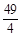
 ,满足
,满足 且
且 ,则
,则 的值为 ▲ .
的值为 ▲ . 过
过 点,且关于
点,且关于 成中心对称.
成中心对称. 的解析式;
的解析式; 满足
满足 .求证:
.求证:
 .
.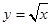 与
与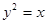
 与
与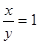
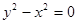 与
与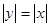
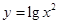 与
与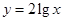
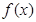 的定义域为
的定义域为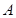 ,若存在非零实数
,若存在非零实数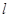 使得对于任意
使得对于任意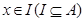 ,有
,有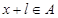 ,且
,且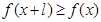 ,则称
,则称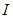 上的
上的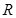 的函数
的函数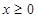 时,
时,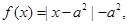 且函数
且函数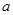 的取值范围为( )
的取值范围为( )