题目内容
1.已知函数f(x)=|x3-4x|+ax-2恰有2个零点,则实数a的取值范围为(-∞,-1)∪(1,+∞).分析 求出y=x3-4x的导数,求得单调区间,根据y=|x3-4x|为偶函数,得到单调区间,画出图象,当直线和曲线在第一象限相切,设切点为(m,n),求得切线的斜率,求得a=-1,m=1,由图象和对称性,可得a>1或a<-1.
解答 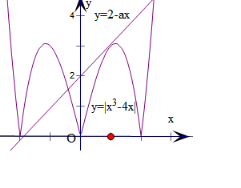 解:由y=x3-4x的导数为y′=3x2-4,
解:由y=x3-4x的导数为y′=3x2-4,
令y′>0,解得x>$\frac{2\sqrt{3}}{3}$,或x<-$\frac{2\sqrt{3}}{3}$,
令y′<0,解得-$\frac{2\sqrt{3}}{3}$x<$\frac{2\sqrt{3}}{3}$,
则y在(-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$)递减,在(-∞,-$\frac{2\sqrt{3}}{3}$),($\frac{2\sqrt{3}}{3}$,+∞)递增,
由于y=|x3-4x|为偶函数,则增区间为(-2,-$\frac{2\sqrt{3}}{3}$),(0,$\frac{2\sqrt{3}}{3}$),(2,+∞),减区间为(-∞,-2),(-$\frac{2\sqrt{3}}{3}$,0),($\frac{2\sqrt{3}}{3}$,2).
作出曲线y=|x3-4x|的图象,以及直线y=2-ax,
当直线和曲线在第一象限相切,设切点为(m,n),
则-a=4-3m2,且2-am=4m-m3,解得a=-1,m=1,
由图象可知,当直线的斜率大于1,即有直线和曲线只有两个交点,
由对称可知,当直线的斜率小于-1,即有直线和曲线只有两个交点.
则a的取值范围是(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
点评 本题考查函数的零点的判断,主要考查数形结合思想方法的运用,同时考查导数的运用:求单调区间,以及函数的对称性,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 7π | B. | 8π | C. | $\frac{28π}{3}$ | D. | $\frac{32π}{3}$ |
| A. | 2 | B. | $\sqrt{3}$或$-\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |

 在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos∠CAD=$\frac{5\sqrt{7}}{14}$.
在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos∠CAD=$\frac{5\sqrt{7}}{14}$. 为了解学生课外阅读的情况,随机统计了n名学生的课外阅读时间,所得数据都在[50,150]中,其频率分布直方图如图所示.已知在[50,75)中的频数为100,则n的值为1000.
为了解学生课外阅读的情况,随机统计了n名学生的课外阅读时间,所得数据都在[50,150]中,其频率分布直方图如图所示.已知在[50,75)中的频数为100,则n的值为1000.