题目内容

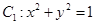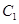在平面直角坐标系xoy中，已知曲线，将上的所有点的横坐标、纵坐标分别伸长为原来的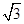、2倍后得到曲线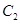，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线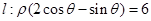

（1）   试写出直线的直角坐标方程；

（2）   在曲线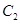上求一点P，使点P到直线的距离最大，并求出此最大值。

 

【答案】

（1）直线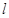的直角坐标方程为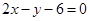：（2）

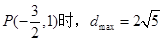
【解析】本试题主要是考查了伸缩变换 运用，以及直角坐标方程中点到直线距离的求解的运用。

（1）因为由题意知，直线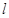的直角坐标方程为：，

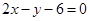（2）那么利用伸缩变换可知曲线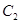的直角坐标方程为：，

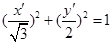点P的坐标可得，结合点到直线的距离公式表示得到三角关系式，借助于三角函数的值域得到最值

 

练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
2
的圆C经过坐标原点O，椭圆
x2
a2
+
y2
9
=1(a＞0)与圆C的一个交点到椭圆两焦点的距离之和为10．
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
3
5
，点B的纵坐标是
12
13
，则sin（α+β）的值是
16
65
16
65
．
在平面直角坐标系xOy中，若焦点在x轴的椭圆
x2
m
+
y2
3
=1的离心率为
1
2
，则m的值为
4
4
．
（2013•泰州三模）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
3t
，0)，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．
（2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1（-1，0），且椭圆C的离心率e=
1
2
．
（1）求椭圆C的方程；
（2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
（3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
16
7
相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网