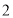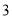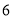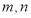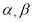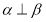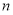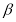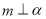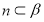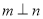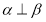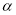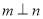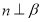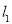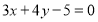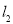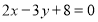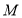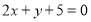题目内容
已知圆 的圆心在直线
的圆心在直线 上,且与直线
上,且与直线 相切于点
相切于点 .
.
(Ⅰ)求圆 方程;
方程;
(Ⅱ)点
 与点
与点 关于直线
关于直线 对称.是否存在过点
对称.是否存在过点 的直线
的直线 ,
,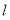 与圆
与圆 相交于
相交于 两点,且使三角形
两点,且使三角形 (
( 为坐标原点),若存在求出直线
为坐标原点),若存在求出直线 的方程,若不存在用计算过程说明理由.
的方程,若不存在用计算过程说明理由.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)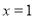
【解析】
试题分析:(Ⅰ)首先求得过圆心与切点的直线,然后与直线 联立可求得圆心,再利用两点间的距离公式可求得半径,进而求得圆的方程;(Ⅱ)首先根据对称性求得
联立可求得圆心,再利用两点间的距离公式可求得半径,进而求得圆的方程;(Ⅱ)首先根据对称性求得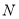 的坐标,然后分直线
的坐标,然后分直线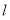 的斜率是否存在两种情况求解,求解过程中注意利用点到直线的距离公式.
的斜率是否存在两种情况求解,求解过程中注意利用点到直线的距离公式.
试题解析:(Ⅰ)过切点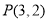 且与
且与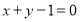 垂直的直线为
垂直的直线为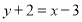 ,即
,即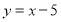 .
.
与直线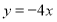 联立可求圆心为
联立可求圆心为 ,
,
所以半径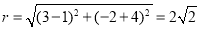 ,
,
所以所求圆的方程为 .
.
(Ⅱ)设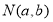 ,∵点
,∵点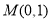 与点
与点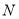 关于直线
关于直线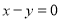 对称,
对称,
∴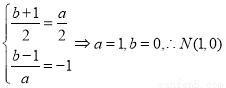 .
.
注意:若没证明,直接得出结果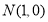 ,不扣分.
,不扣分.
1.当斜率不存在时,此时直线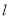 方程为
方程为 ,原点到直线的距离为
,原点到直线的距离为 ,
,
同时令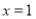 代人圆方程得
代人圆方程得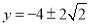 ,∴
,∴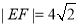 ,
,
∴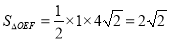 满足题意,此时方程为
满足题意,此时方程为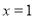 .
.
2.当斜率存在时,设直线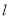 的方程为
的方程为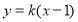 ,即
,即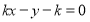 ,
,
圆心 到直线
到直线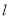 的距离
的距离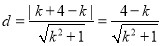 ,
,
设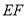 的中点为
的中点为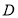 ,连接
,连接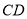 ,则必有
,则必有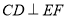 ,
,
在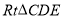 中,
中,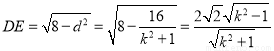 ,所以
,所以 ,
,
而原点到直线的距离为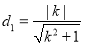 ,所以
,所以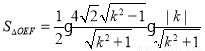
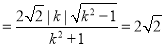 ,
,
整理,得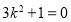 ,不存在这样的实数
,不存在这样的实数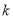 ,
,
综上所述直线的方程为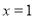 .
.
考点:1.直线与圆的位置关系;2、点到直线的距离

练习册系列答案
相关题目