题目内容
13.|$\overrightarrow{a}$|=4,$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为30°,则|$\overrightarrow{b}$|的最小值为2.分析 设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$,由几何意义得知当OB⊥AB时OB最短,求出最值.
解答 解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$,如图,则∠A=30°,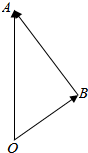
所以当OB⊥AB时OB最短,即|$\overrightarrow{b}$|的最小值为:|OA|×sin30°=$|\overrightarrow{a}|sin30°$=4×$\frac{1}{2}$=2;
故答案为:2.
点评 本题考查了平面向量是几何意义的运用;关键是画出图形,利用几何意义解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.与直线y=$\frac{1}{2}$x+3平行且过点(0,-1)的直线方程为( )
| A. | 2x+y+1=0 | B. | x+2y+2=0 | C. | x-2y-2=0 | D. | 2x-y-1=0 |
18.设集合A={x|2<x<5},B={x|x<b},若A⊆B,则b的取值范围是( )
| A. | b≤2 | B. | b≤5 | C. | b≥2 | D. | b≥5 |
5.△ABC中,三个角A,B,C所对的边a,b,c满足a2+b2=c2-$\sqrt{3}$ab,则C=( )
| A. | 150° | B. | 135° | C. | 120° | D. | 60° |