题目内容
已知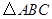 的三个内角
的三个内角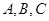 所对边长分别为
所对边长分别为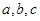 ,向量
,向量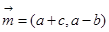 ,
,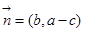 ,若
,若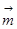 ∥
∥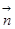 ,则
,则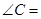 ( )
( )
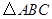 的三个内角
的三个内角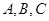 所对边长分别为
所对边长分别为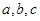 ,向量
,向量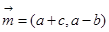 ,
,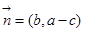 ,若
,若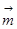 ∥
∥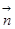 ,则
,则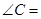 ( )
( )A.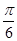 | B.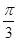 | C.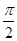 | D.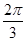 |
B
试题分析:根据题意中向量共线可知满足坐标关系式为(a-c)(a+c)-b(a-b)=0,a
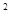 -c
-c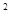 +b
+b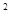 -ab=0,进而得到角C的余弦值为
-ab=0,进而得到角C的余弦值为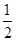 ,那么结合余弦定理可知角C的值为
,那么结合余弦定理可知角C的值为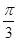 ,选B.
,选B.点评:主要是考查了向量共线以及解三角形的运用,属于基础题。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
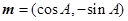 ,
,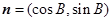 ,
,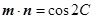 ,其中
,其中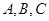 为
为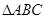 的内角.
的内角.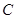 的大小;
的大小;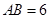 ,且
,且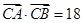 ,求
,求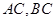 的长.
的长.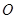 为
为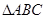 内一点,若对任意
内一点,若对任意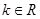 ,恒有
,恒有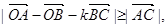 则
则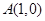 和点
和点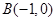 ,
,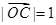 ,且
,且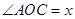 ,其中
,其中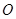 为坐标原点.
为坐标原点.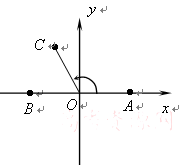
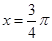 ,设点
,设点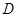 为线段
为线段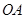 上的动点,求
上的动点,求 的最小值;
的最小值;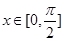 ,向量
,向量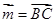 ,
,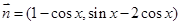 ,求
,求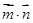 的最小值及对应的
的最小值及对应的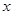 值.
值.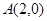 ,
,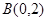 ,
,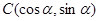 ,
,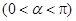 .
.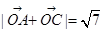 (
(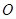 为坐标原点),求
为坐标原点),求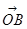 与
与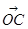 的夹角;
的夹角;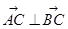 ,求
,求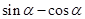 的值.
的值.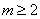 ,点
,点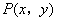 为
为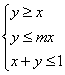 所表示的平面区域内任意一点,
所表示的平面区域内任意一点,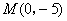 ,
,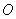 为坐标原点,
为坐标原点,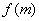 为
为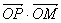 的最小值,则
的最小值,则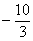

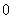

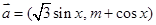 ,
,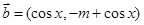 , 且
, 且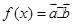
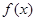 的最小正周期
的最小正周期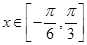 时,
时, 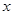 的值.
的值.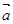 、
、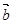 、
、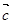 是同一平面的三个单位向量,且
是同一平面的三个单位向量,且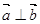 , 则
, 则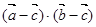 的最小值为( )
的最小值为( )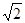
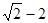
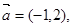 又点
又点
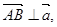 求向量
求向量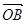 的坐标;
的坐标;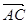 与向量
与向量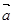 共线,当
共线,当 取最大值时,求
取最大值时,求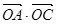 .
.