Question

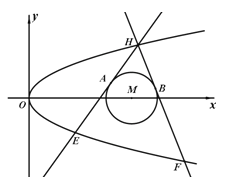
【题目】如图，已知抛物线：和⊙ ，过抛线上一点 作两条直线与⊙相切于A、B两点，分别交抛物线于E、F两点，圆心点到抛物线准线的距离为 ．

（Ⅰ）求抛物线的方程；

（Ⅱ）当 的角平分线垂直x轴时，求直线EF的斜率；

（Ⅲ）若直线AB在轴上的截距为，求的最小值．

Answer 1

【答案】（Ⅰ） ;（Ⅱ）-;（Ⅲ）-11.

【解析】

（Ⅰ）由即可得解；

（Ⅱ）当的角平分线垂直轴时，点 ，由及化简即可得解；

（Ⅲ）设点 ，以为圆心，为半径的圆方程为 与⊙方程：相减可得直线，令利用函数单调性即可得解.

（Ⅰ）∵点到抛物线准线的距离为 ，

∴ ，即抛物线的方程为．

（Ⅱ）∵当的角平分线垂直轴时，点 ，

∴

设 ， ，

∴ ， ∴

∴ ．

．

（Ⅲ）设点 ， ，．

以为圆心，为半径的圆方程为 ，……①

⊙方程：．……②

①-②得：

直线的方程为 ．

当时，直线在轴上的截距 ，

∵关于的函数在单调递增， ∴．