题目内容
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当直线垂直于
两点,当直线垂直于![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的方程
的方程
(2)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形?若存在,求出
为底的等腰三角形?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,见解析
,见解析
【解析】
(1)根据题意可得关于a,b,c的方程组,求出a,b,c即可求椭圆的方程;
(2)设出直线方程,联立直线方程和椭圆方程,转化为一元二次方程,利用根与系数之间的关系进行求解.
(1)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当直线垂直于
两点,当直线垂直于![]() 轴时,
轴时,![]() .
.
得椭圆![]() 过点
过点![]() ,得
,得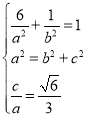 ,
,
解得![]() ,所以椭圆的
,所以椭圆的![]() 方程为:
方程为:![]() .
.
(2)设![]() ,
,![]() 的中点
的中点![]() .
.
由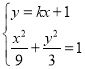 ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
①当![]() 时,线段
时,线段![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() .
.
令![]() ,得
,得![]() ,即
,即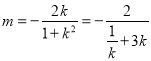 .
.
若![]() ,则
,则![]() ,那么
,那么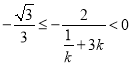 ;
;
若![]() ,则
,则![]() ,
,
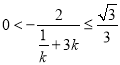 ,所以
,所以![]() 或
或![]() .
.
②当![]() 时,
时,![]() .
.
综上所述,存在点![]() 满足条件,
满足条件,![]() 取值范围是
取值范围是![]() .
.

【题目】某工厂36名工人的年龄数据如下表.
工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | |||
1 | 40 | 10 | 36 | 19 | 27 | 28 | 34 | |||
2 | 44 | 11 | 31 | 20 | 43 | 29 | 39 | |||
3 | 40 | 12 | 38 | 21 | 41 | 30 | 43 | |||
4 | 41 | 13 | 39 | 22 | 37 | 31 | 38 | |||
5 | 33 | 14 | 43 | 23 | 34 | 32 | 42 | |||
6 | 40 | 15 | 45 | 24 | 42 | 33 | 53 | |||
7 | 45 | 16 | 39 | 25 | 37 | 34 | 37 | |||
8 | 42 | 17 | p>38 | 26 | 44 | 35 | 49 | |||
9 | 43 | 18 | 36 | 27 | 42 | 36 | 39 |
若从36名工人中抽取容量为9的样本,样本的年龄数据是44,40,36,43,36,37,44,43,37.
(1)计算样本的平均数x和方差![]() .
.
(2)36名工人中年龄在![]() 与
与![]() 之间的有多少人?所占的百分比是多少(精确到0.01%)?
之间的有多少人?所占的百分比是多少(精确到0.01%)?
【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):

(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
