题目内容
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(1)证明:BD⊥AA1;
(2)求锐二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(1)证明见解析;(2) 二面角D-A1A-C的平面角的余弦值是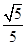 .(3)存在,点P在C1C的延长线上且使C1C=CP.
.(3)存在,点P在C1C的延长线上且使C1C=CP.
解析试题分析:(1)连接BD交AC于O,则BD⊥AC,连接A1O,可证A1O⊥底面ABCD,则可建立如图所示的空间直角坐标系,分别写出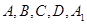 的坐标,进而得
的坐标,进而得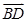 ,
, 坐标,由坐标运算可得
坐标,由坐标运算可得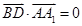 ,即两向量垂直,得两线垂直;(2)分别求出两平面的一个法向量
,即两向量垂直,得两线垂直;(2)分别求出两平面的一个法向量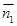 ,
,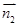 ,利用
,利用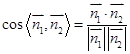 ,可得二面角的平面角的余弦值;(3)令存在,在直线CC1 上设
,可得二面角的平面角的余弦值;(3)令存在,在直线CC1 上设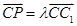 ,P(x,y,z),得
,P(x,y,z),得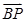 =(
=(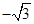 ,1+λ,
,1+λ,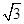 λ),取平面DA1C一法向量
λ),取平面DA1C一法向量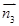 ,知
,知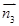 ·
·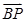 =0,得
=0,得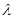 的值,P点可求.
的值,P点可求.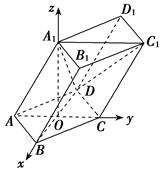
解:连接BD交AC于O,则BD⊥AC,连接A1O.
在△AA1O中,AA1=2,AO=1,∠A1AO=60°,
∴A1O2=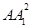 +AO2-2AA1·AOcos 60°=3,
+AO2-2AA1·AOcos 60°=3,
∴AO2+A1O2=A1A2,∴A1O⊥AO,
由于平面AA1C1C⊥平面ABCD,∴A1O⊥底面ABCD, 2分
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B(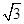 ,0,0),C(0,1,0),D(
,0,0),C(0,1,0),D(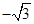 ,0,0),A1(0,0,
,0,0),A1(0,0,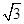 ).
).
(1)由于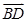 =(
=(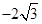 ,0,0),
,0,0), =(0,1,
=(0,1,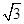 ),则
),则 ·
·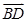 =0×(
=0×(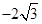 )+1×0+
)+1×0+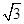 ×0=0,
×0=0,
所以:BD⊥AA1. 4分
(2)由于OB⊥平面AA1C1C,
∴平面AA1C1C的法向量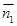 =(1,0,0),设
=(1,0,0),设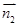 ⊥平面AA1D,则
⊥平面AA1D,则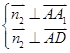
设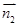 =(x,y,z),
=(x,y,z),
得到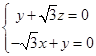 取
取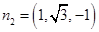 , 6分
, 6分
∴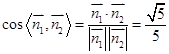 ,
,
∴二面角D-A1A-C的平面角的余弦值是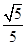 . 8分
. 8分
(3)假设在直线CC1上存在点P,使BP∥平面DA1C1,
设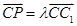 ,P(x,y,z),则(x,y-1,z)=λ(0,1,
,P(x,y,z),则(x,y-1,z)=λ(0,1,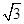 ), 9分
), 9分
得P(0,1+λ,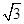 λ),
λ),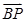 =(
=(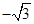 ,1+λ,
,1+λ,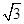 λ).
λ).
设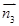 ⊥平面DA1C1,则
⊥平面DA1C1,则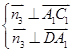 .
.
设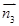 =(x3,y3,z3),得到
=(x3,y3,z3),得到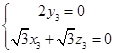 .
.
不妨取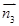 =(1,0,-1). 10分
=(1,0,-1). 10分
又∵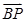 ∥平面DA1C1,则
∥平面DA1C1,则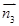 ·
·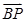 =0,即
=0,即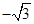 -
-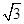

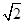 a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.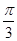 .
.
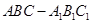 中,平面
中,平面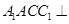 平面ABC,
平面ABC,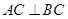 ,
,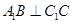 ,
,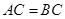 .
.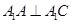 ;
;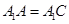 ,求二面角
,求二面角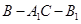 的余弦值.
的余弦值.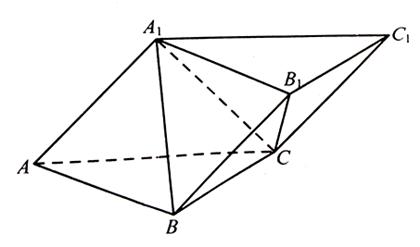
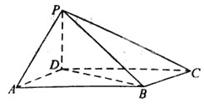
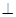 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD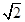 ,M为棱PB的中点.
,M为棱PB的中点.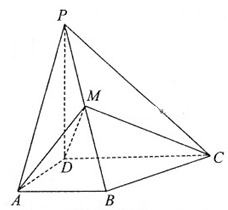
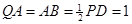 .
.