题目内容
已知函数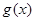 =
=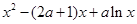 。
。
(1)当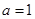 时,求函数
时,求函数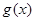 的单调增区间;
的单调增区间;
(2)求函数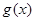 在区间
在区间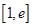 上的最小值;
上的最小值;
(3)在(1)的条件下,设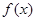 =
=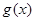 +
+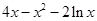 ,
,
求证: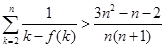 (
(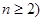 ),参考数据:
),参考数据: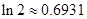 。(13分)
。(13分)
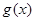 =
=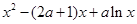 。
。(1)当
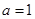 时,求函数
时,求函数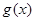 的单调增区间;
的单调增区间;(2)求函数
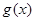 在区间
在区间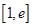 上的最小值;
上的最小值;(3)在(1)的条件下,设
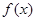 =
=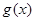 +
+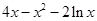 ,
,求证:
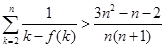 (
(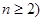 ),参考数据:
),参考数据: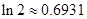 。(13分)
。(13分)(1)单调增区间是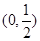 ,
,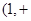
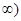 ;
;
(2)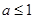 时,
时,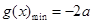 ;
;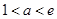 时,
时,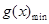 =
=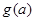 =
=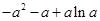 ;
;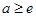 时,
时,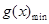 =
=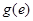 =
=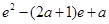 .
.
(3)证明详见解析.
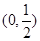 ,
,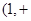
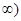 ;
;(2)
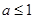 时,
时,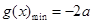 ;
;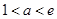 时,
时,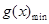 =
=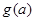 =
=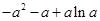 ;
;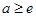 时,
时,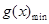 =
=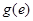 =
=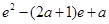 .
.(3)证明详见解析.
试题分析:(1)求f(x)的导函数f′(x),讨论a的值使f′(x)>0时对应f(x)单调增,
f′(x)<0时,对应f(x)单调减;
(2)结合(1),讨论a的取值对应f(x)在区间[1,e]内的单调性,从而求得f(x)在区间[1,e]内的最小值.
试题解析:(1)当
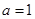 时,
时,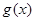 =
=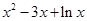 ,
,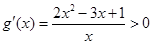 ,得
,得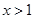 或
或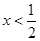 ,故
,故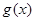 的单调增区间是
的单调增区间是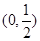 ,
,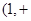
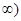 。 3分
。 3分(2)
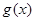 =
=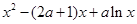 ,
,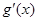 =
= =
=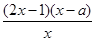 ,
,令
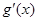 =0得
=0得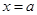 或
或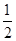
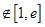 。
。当
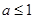 时,
时,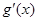
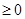 ,
,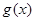 递增,
递增,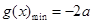 ; 6分
; 6分当
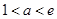 时,
时,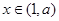 ,
,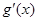 <0,
<0,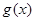 递减;
递减;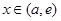 ,
,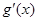
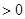 ,
,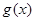 递增,
递增,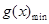 =
=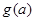 =
=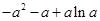 7分
7分当
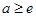 时,
时,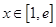 ,
,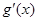
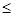 0,
0,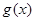 递减,
递减,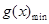 =
=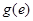 =
=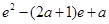 …8分
…8分(3)令
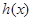 =
=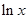 —
—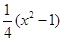 ,
,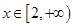 。
。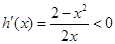 ,
,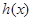 递减,
递减,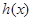
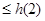 ,
,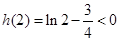 ,∴
,∴ 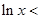
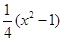 ,
,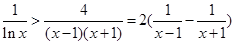
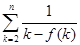 =
=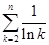 =
=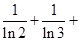 …
…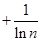

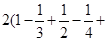 …
…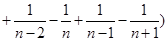 =
=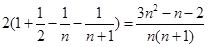 (
(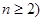 )……13分
)……13分
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
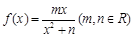 , 在
, 在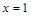 处取得极小值2.
处取得极小值2.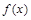 的解析式;
的解析式;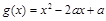 , 若对于任意
, 若对于任意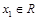 ,总存在
,总存在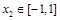 , 使得
, 使得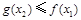 , 求实数
, 求实数 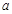 的取值范围.
的取值范围.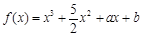 (
(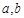 为常数),其图象是曲线
为常数),其图象是曲线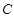 .
.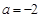 时,求函数
时,求函数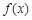 的单调减区间;
的单调减区间;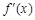 ,若存在唯一的实数
,若存在唯一的实数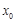 ,使得
,使得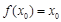 与
与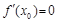 同时成立,求实数
同时成立,求实数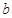 的取值范围;
的取值范围;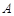 为曲线
为曲线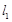 与曲线
与曲线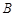 ,在点
,在点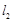 ,设切线
,设切线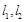 的斜率分别为
的斜率分别为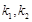 .问:是否存在常数
.问:是否存在常数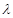 ,使得
,使得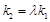 ?若存在,求出
?若存在,求出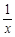 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 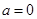 时,求
时,求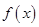 的极值;
的极值;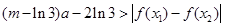 成立,求实数m的取值范围。
成立,求实数m的取值范围。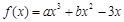
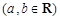 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.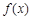 的解析式;
的解析式;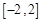 上任意两个自变量的值
上任意两个自变量的值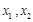 ,都有
,都有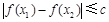 ,求实数
,求实数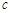 的最小值;
的最小值;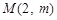
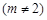 ,可作曲线
,可作曲线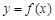 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.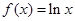 ,
,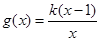 .
.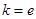 时,求函数
时,求函数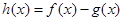 的单调区间和极值;
的单调区间和极值;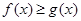 恒成立,求实数
恒成立,求实数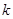 的值.
的值.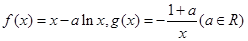 .
. 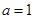 时,求曲线
时,求曲线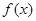 在
在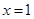 处的切线方程;
处的切线方程;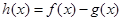 ,求函数
,求函数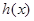 的单调区间;
的单调区间;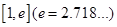 上存在一点
上存在一点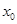 ,使得
,使得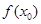 <
<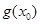 成立,求
成立,求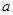 的取值范围.
的取值范围.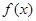 的导函数图象如图所示,若
的导函数图象如图所示,若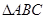 为锐角三角形,则一定成立的是( )
为锐角三角形,则一定成立的是( )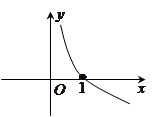
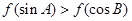
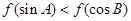
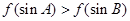
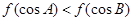
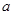 为常数,函数
为常数,函数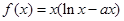 有两个极值点
有两个极值点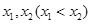 ,则( )
,则( )