题目内容
(本小题满分12分)已知函数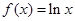 ,
,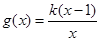 .
.
(1)当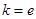 时,求函数
时,求函数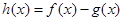 的单调区间和极值;
的单调区间和极值;
(2)若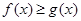 恒成立,求实数
恒成立,求实数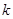 的值.
的值.
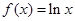 ,
,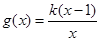 .
.(1)当
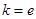 时,求函数
时,求函数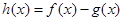 的单调区间和极值;
的单调区间和极值;(2)若
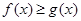 恒成立,求实数
恒成立,求实数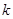 的值.
的值.(1)函数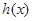 的减区间为
的减区间为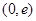 ,增区间为
,增区间为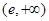 ,极小值为
,极小值为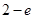 ,无极大值;(2)
,无极大值;(2)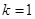 .
.
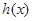 的减区间为
的减区间为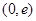 ,增区间为
,增区间为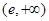 ,极小值为
,极小值为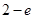 ,无极大值;(2)
,无极大值;(2)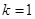 .
.试题分析:本题综合考察函数与导数及运用导数求单调区间、极值、最值等数学知识和方法,突出考查综合运用数学知识和方法分析问题、解决问题的能力.第一问,将
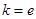 代入,先得到
代入,先得到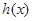 的表达式,注意到定义域中
的表达式,注意到定义域中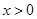 ,对
,对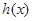 求导,根据
求导,根据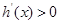 ,判断出
,判断出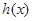 的单调增区间,
的单调增区间,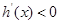 ,判断出
,判断出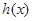 的单调减区间,通过单调性判断出极值的位置,求出极值;第二问,先将
的单调减区间,通过单调性判断出极值的位置,求出极值;第二问,先将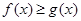 恒成立转化为
恒成立转化为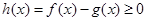 恒成立,所以整个这一问只需证明
恒成立,所以整个这一问只需证明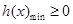 即可,对
即可,对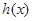 求导,由于
求导,由于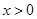 ,所以须讨论
,所以须讨论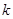 的正负,当
的正负,当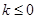 时,
时,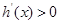 ,所以判断出
,所以判断出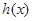 在
在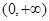 上为增函数,但是
上为增函数,但是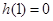 ,所以当
,所以当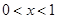 时,
时,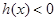 不符合题意,当
不符合题意,当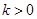 时,判断出
时,判断出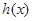 在
在 上为减函数,
上为减函数,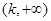 上为增函数,但是
上为增函数,但是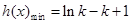 ,必须证明出
,必须证明出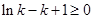 ,所以再构造新函数
,所以再构造新函数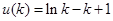 ,判断
,判断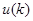 函数的最值,只有
函数的最值,只有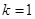 时符合
时符合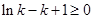 .
.试题解析:⑴解:注意到函数
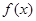 的定义域为
的定义域为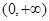 ,
,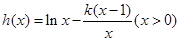 ,
,当
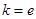 时,
时, 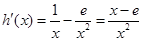 , 2分
, 2分若
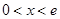 ,则
,则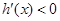 ;若
;若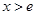 ,则
,则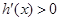 .
.所以
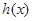 是
是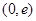 上的减函数,是
上的减函数,是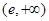 上的增函数,
上的增函数,故
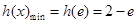 ,
,故函数
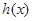 的减区间为
的减区间为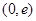 ,增区间为
,增区间为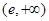 ,极小值为
,极小值为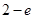 ,无极大值.---5分
,无极大值.---5分⑵解:由⑴知
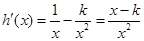 ,
,当
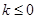 时,
时,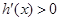 对
对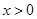 恒成立,所以
恒成立,所以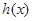 是
是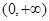 上的增函数,
上的增函数,注意到
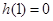 ,所以
,所以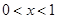 时,
时,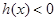 不合题意. 7分
不合题意. 7分当
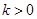 时,若
时,若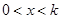 ,
,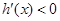 ;若
;若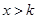 ,
,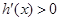 .
.所以
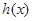 是
是 上的减函数,是
上的减函数,是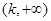 上的增函数,
上的增函数,故只需
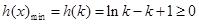 . 9分
. 9分令
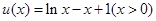 ,
,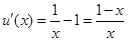 ,
,当
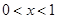 时,
时,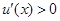 ; 当
; 当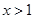 时,
时,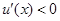 .
.所以
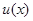 是
是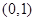 上的增函数,是
上的增函数,是 上的减函数.
上的减函数.故
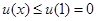 当且仅当
当且仅当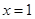 时等号成立.
时等号成立.所以当且仅当
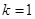 时,
时,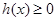 成立,即
成立,即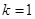 为所求. 12分
为所求. 12分
练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
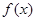 是二次函数,不等式
是二次函数,不等式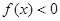 的解集是
的解集是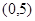 ,且
,且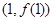 处的切线与直线
处的切线与直线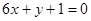 平行.
平行.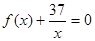 在区间
在区间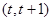 内有两个不等的实数根?
内有两个不等的实数根?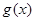 =
=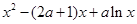 。
。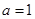 时,求函数
时,求函数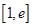 上的最小值;
上的最小值;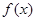 =
=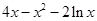 ,
,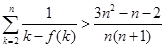 (
(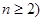 ),参考数据:
),参考数据: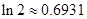 。(13分)
。(13分)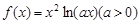
 时,求
时,求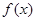 在
在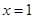 处的切线方程;
处的切线方程;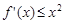 对任意的
对任意的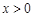 恒成立,求实数
恒成立,求实数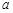 的取值范围;
的取值范围;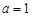 时,设函数
时,设函数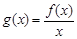 ,若
,若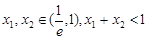 ,求证:
,求证: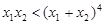 .
.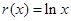 ,函数
,函数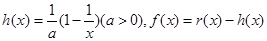 .
.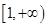 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围: 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列 的前n项和为
的前n项和为 ,求证:当
,求证:当 时,
时,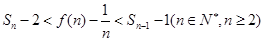 .
. 在
在 与
与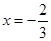 时,都取得极值.
时,都取得极值.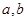 的值;
的值;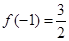 ,求
,求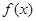 的单调区间和极值;
的单调区间和极值;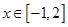 都有
都有 恒成立,求
恒成立,求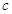 的取值范围.
的取值范围.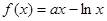 在
在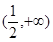 内单调递增,则
内单调递增,则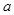 的取值范围为( )
的取值范围为( )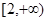
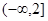
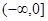
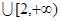
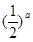 =
=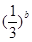 ,则a>b>0;
,则a>b>0;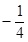 ;
;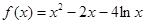 ,则
,则 的解集为 。
的解集为 。