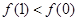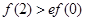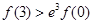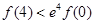题目内容
已知函数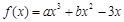
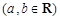 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
⑴求函数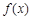 的解析式;
的解析式;
⑵若对于区间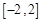 上任意两个自变量的值
上任意两个自变量的值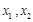 ,都有
,都有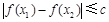 ,求实数
,求实数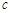 的最小值;
的最小值;
⑶若过点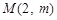
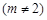 ,可作曲线
,可作曲线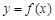 的三条切线,求实数
的三条切线,求实数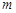 的取值范围.
的取值范围.
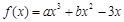
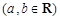 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.⑴求函数
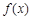 的解析式;
的解析式;⑵若对于区间
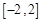 上任意两个自变量的值
上任意两个自变量的值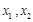 ,都有
,都有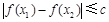 ,求实数
,求实数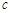 的最小值;
的最小值;⑶若过点
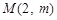
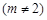 ,可作曲线
,可作曲线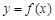 的三条切线,求实数
的三条切线,求实数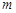 的取值范围.
的取值范围.⑴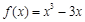 ;⑵
;⑵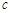 的最小值为
的最小值为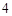 ;⑶
;⑶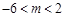 .
.
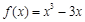 ;⑵
;⑵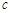 的最小值为
的最小值为 ;⑶
;⑶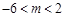 .
.试题分析:⑴
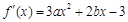 ,由
,由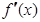 是偶函数得
是偶函数得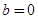 .又
.又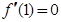 ,所以
,所以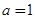 ,由此可得解析式;
,由此可得解析式;⑵对于区间
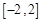 上任意两个自变量的值
上任意两个自变量的值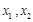 ,都有
,都有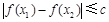 ,则只需
,则只需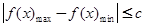 即可.所以接下来就利用导数求
即可.所以接下来就利用导数求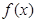 在区间
在区间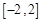 上的最大值与最小值,然后代入
上的最大值与最小值,然后代入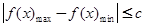 解不等式即可得
解不等式即可得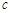 的最小值.⑶易知点
的最小值.⑶易知点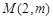
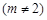 不在曲线
不在曲线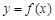 上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..
上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..设切点为
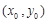 .则
.则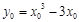 .又
.又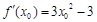 ,∴切线的斜率为
,∴切线的斜率为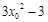 .
.由此得
 ,即
,即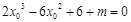 .下面就考查这个方程的解的个数.
.下面就考查这个方程的解的个数.因为过点
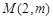
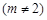 ,可作曲线
,可作曲线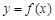 的三条切线,所以方程
的三条切线,所以方程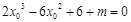 有三个不同的实数解.即函数
有三个不同的实数解.即函数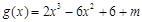 有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数.
有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数. 试题解析:⑴∵
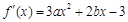 ,1分
,1分由
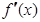 是偶函数得
是偶函数得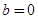 .又
.又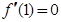 ,所以
,所以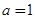 3分
3分∴
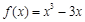 .4分
.4分⑵令
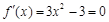 ,即
,即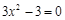 ,解得
,解得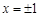 .5分
.5分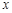 | 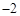 | 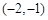 | 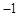 | 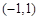 | 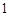 | 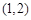 |  |
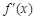 | | 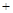 |  | 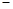 |  | + | |
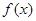 | 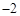 | 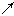 | 极大值 | 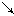 | 极小值 |  |  |
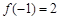 ,
,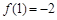 ,
,∴当
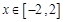 时,
时,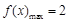 ,
,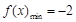 .6分
.6分则对于区间
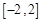 上任意两个自变量的值
上任意两个自变量的值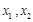 ,都有
,都有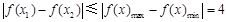 ,所以
,所以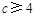 .
.所以
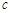 的最小值为
的最小值为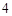 .8分
.8分⑶∵点
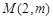
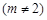 不在曲线
不在曲线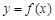 上,
上,∴设切点为
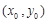 .则
.则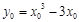 .
.∵
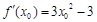 ,∴切线的斜率为
,∴切线的斜率为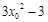 .
.则
 ,即
,即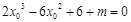 .10分
.10分因为过点
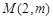
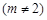 ,可作曲线
,可作曲线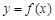 的三条切线,
的三条切线,所以方程
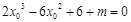 有三个不同的实数解.
有三个不同的实数解.即函数
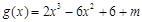 有三个不同的零点.11分
有三个不同的零点.11分则
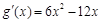 .
.令
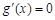 ,解得
,解得 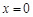 或
或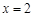 .
.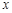 | 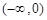 |  | 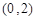 | 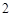 | 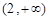 |
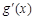 | + |  | 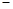 |  | + |
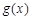 | 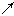 | 极大值 | 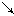 | 极小值 | 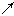 |
 即
即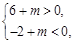 解得
解得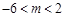 .12分
.12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
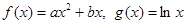 .
.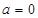 时,①若
时,①若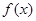 的图象与
的图象与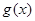 的图象相切于点
的图象相切于点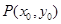 ,求
,求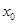 及
及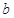 的值;
的值;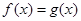 在
在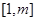 上有解,求
上有解,求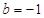 时,若
时,若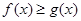 在
在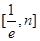 上恒成立,求
上恒成立,求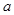 的取值范围.
的取值范围.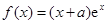 ,其中
,其中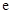 是自然对数的底数,
是自然对数的底数,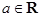 .
.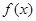 的单调区间;
的单调区间;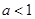 时,试确定函数
时,试确定函数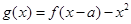 的零点个数,并说明理由.
的零点个数,并说明理由.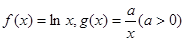 ,设
,设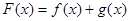
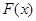 的单调区间
的单调区间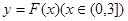 图象上任意一点
图象上任意一点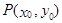 为切点的切线的斜率
为切点的切线的斜率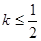 恒成立,求实数
恒成立,求实数 的最小值
的最小值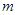 ,使得函数
,使得函数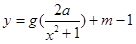 的图象与函数
的图象与函数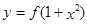 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数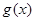 =
=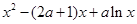 。
。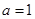 时,求函数
时,求函数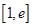 上的最小值;
上的最小值;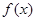 =
=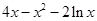 ,
,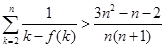 (
(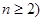 ),参考数据:
),参考数据: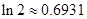 。(13分)
。(13分)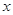 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量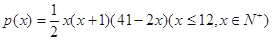 (单位:件)
(单位:件)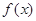 的表达式;
的表达式;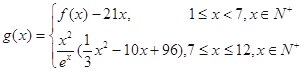 (单位:件),每件利润
(单位:件),每件利润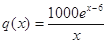 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: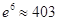 )
)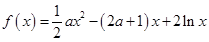 .
.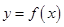 在
在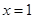 和
和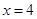 处的切线相互平行,求
处的切线相互平行,求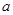 的值;
的值;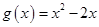 ,对任意的
,对任意的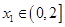 ,均存在
,均存在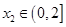 ,使得
,使得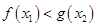 .试求实数
.试求实数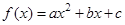 的导数
的导数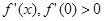 ,且
,且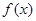 的值域为
的值域为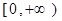 ,则
,则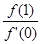 的最小值为( )
的最小值为( )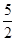
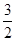
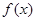 在
在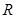 上可导,其导函数为
上可导,其导函数为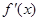 ,若
,若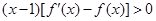 ,
,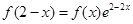 ,则下列判断一定正确的是 ( )
,则下列判断一定正确的是 ( )