题目内容
18.已知定义在R上的偶函数f(x)在x≥0时,f(x)=ex+$\sqrt{x}$,若f(a)<f(a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,+∞) |
分析 由已知得到f(x)在[0,+∞)上为增函数,从而由f(x)为偶函数及f(a)<f(a-1)得到f(|a|)<f(|a-1|),从而得到|a|<|a-1|,解该不等式即得a的取值范围.
解答 解:∵偶函数f(x)在x≥0时,f(x)=ex+$\sqrt{x}$为增函数,
∴若f(a)<f(a-1),则f(|a|)<f(|a-1|),
即|a|<|a-1|;
∴解得a<$\frac{1}{2}$.
∴a的取值范围是(-∞,$\frac{1}{2}$).
故选:B
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的性质,是解答的关键.

练习册系列答案
相关题目
9. 如图,在棱长为3的正方体ABCD-A1B1C1D1中,M为线段B1C1上的动点,则三棱锥M-BCD1的体积为( )(参考结论:若一条直线与一个平面平行,则该直线上的动点到此平面的距离是一个定值)
如图,在棱长为3的正方体ABCD-A1B1C1D1中,M为线段B1C1上的动点,则三棱锥M-BCD1的体积为( )(参考结论:若一条直线与一个平面平行,则该直线上的动点到此平面的距离是一个定值)
 如图,在棱长为3的正方体ABCD-A1B1C1D1中,M为线段B1C1上的动点,则三棱锥M-BCD1的体积为( )(参考结论:若一条直线与一个平面平行,则该直线上的动点到此平面的距离是一个定值)
如图,在棱长为3的正方体ABCD-A1B1C1D1中,M为线段B1C1上的动点,则三棱锥M-BCD1的体积为( )(参考结论:若一条直线与一个平面平行,则该直线上的动点到此平面的距离是一个定值)| A. | 3 | B. | $\frac{9}{2}$ | C. | 9 | D. | 与M点的位置有关 |
13.已知函数f(x)=|cosx|•sinx,给出下列四个说法,其中正确说法是( )
| A. | 若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z) | B. | f(x)在区间$[-\frac{π}{4},\frac{π}{4}]$上单调递增 | ||
| C. | 函数f(x)的周期为π | D. | f(x)的图象关于点$(-\frac{π}{2},0)$成中心对称 |
7.抛物线y2=8x的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足$∠AFB=\frac{2π}{3}$,过线段AB的中点M作直线l的垂线,垂足为N,则$\frac{|MN|}{|AB|}$的最大值,是( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
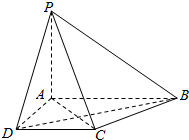 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,PA=$\sqrt{3}$,∠BAD=120°,∠ACB=90°.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,PA=$\sqrt{3}$,∠BAD=120°,∠ACB=90°.