题目内容
9.某工厂生产某种产品,成本C(单位:万元)与年产量x,(0≤x≤15,单位:千台)的函数关系为C(x)=2-x.销售收入S:(单位:万元)与年产量x有函数关系S(x)=$-{\frac{1}{3}x}^{2}$+5x.(1)试求利润y与产量x的关系式;
(2)年产量为多少台时利润最大,最大利润是多少?(总利润=总收益-总成本).
分析 (1)利用“总利润=总收益-总成本”代入计算即得结论;
(2)通过(1)结合函数y=$-{\frac{1}{3}x}^{2}$+6x-2的图象及0≤x≤15可知当x=9时y取最大值,进而计算即得结论.
解答 解:(1)∵总利润=总收益-总成本,
∴y=S(x)-C(x)=$-{\frac{1}{3}x}^{2}$+5x-(2-x)=$-{\frac{1}{3}x}^{2}$+6x-2(0≤x≤15);
(2)由(1)可知函数y=$-{\frac{1}{3}x}^{2}$+6x-2的图象是以x=-$\frac{6}{2×(-\frac{1}{3})}$=9为对称轴、开口向下的抛物线,
又∵0≤x≤15,
∴当x=9时,y取最大值-$\frac{1}{3}$×92+6×9-2=25,
∴年产量为9千台时利润最大,最大利润是25万元.
点评 本题是一道关于函数的简单应用题,考查分析问题、解决问题的能力,注意解题方法的积累,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第39颗珠子的颜色是( )
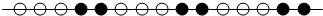
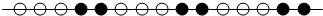
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈R),则“$φ=\frac{π}{2}$”是“f(x)是偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |