题目内容
3.已知函数f(x)在区间(0,+∞)上是单调递减的,试比较f(a2-a+1)与$f(\frac{3}{4})$的大小f(a2-a+1)$≤f(\frac{3}{4})$.分析 根据二次函数最小值的求解公式可得到${a}^{2}-a+1≥\frac{3}{4}$,从而由f(x)在(0,+∞)上单调递减便可判断f(a2-a+1)与$f(\frac{3}{4})$的大小关系.
解答 解:${a}^{2}-a+1≥\frac{4-1}{4}=\frac{3}{4}$;
∵f(x)在区间(0,+∞)上单调递减;
∴$f({a}^{2}-a+1)≤f(\frac{3}{4})$.
故答案为:$f({a}^{2}-a+1)≤f(\frac{3}{4})$.
点评 考查二次函数最小值的计算公式,以及减函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.己知函数f(x)与它的导函数f'(x)满足x2f'(x)+xf(x)=lnx,且f(e)=$\frac{1}{e}$,则下列结论正确的是( )
| A. | f(x)在区间(0,+∞)上是减函数 | B. | f(x)在区间(0,+∞)上是增函数 | ||
| C. | f(x)在区间(0,+∞)上先增后减 | D. | f(x)在区间(0,+∞)上是先减后增 |
12.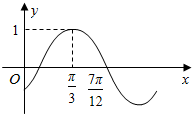 已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )
已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )
 已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )
已知函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )| A. | ω=1,φ=$\frac{π}{6}$ | B. | ω=1,φ=-$\frac{π}{6}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=2,φ=-$\frac{π}{6}$ |
13.函数f(x)=sin(x+$\frac{π}{6}$)的一个递减区间是( )
| A. | [-$\frac{π}{2}$,$\frac{π}{2}$] | B. | [-π,0] | C. | [-$\frac{2}{3}π$,$\frac{2}{3}π$] | D. | [$\frac{π}{2}$,$\frac{2}{3}π$] |
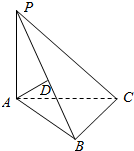 在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,求证:AD⊥面BPC.
在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,求证:AD⊥面BPC.