题目内容
8.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.(1)求椭圆C的方程:
(2)若直线L与椭圆C交于不同的两点A,B,且线段AB的中点N(1,1),求直线L的方程.
分析 (1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得即可得出.
(2)设A(x1,y1),B(x2,y2).代入椭圆方程可得:$\frac{{x}_{1}^{2}}{8}+\frac{{y}_{1}^{2}}{4}=1$,$\frac{{x}_{2}^{2}}{8}+\frac{{y}_{2}^{2}}{4}$=1,两式相减并且利用中点坐标公式与斜率计算公式可得$\frac{2}{8}+\frac{2k}{4}$=0,解得k即可得出.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=8,b2=c2=4.
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
(2)设A(x1,y1),B(x2,y2).
代入椭圆方程可得:$\frac{{x}_{1}^{2}}{8}+\frac{{y}_{1}^{2}}{4}=1$,$\frac{{x}_{2}^{2}}{8}+\frac{{y}_{2}^{2}}{4}$=1,
两式相减可得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{8}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{4}$=0,
又x1+x2=2,y1+y2=2,$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=k,
可得$\frac{2}{8}+\frac{2k}{4}$=0,解得k=$-\frac{1}{2}$.
∴直线L的方程为y-1=$-\frac{1}{2}$(x-1),
化为:x+2y-3=0.
点评 本题考查了椭圆的标准方程及其性质、“点差法”、点斜式、中点坐标公式、斜率计算公式,考查了推理能力与计算能力,属于难题.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | $\sqrt{2}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{3}$-1 |
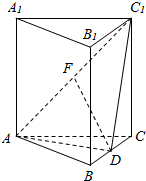 如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.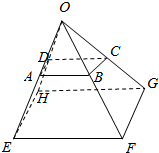 已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证:
已知O、A、B、C、D、F、F、G、H为空间9个点(如图),并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$,$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$.求证: