Question

15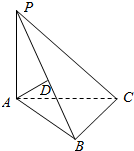．在三棱锥P-ABC中，PA⊥面ABC，∠ABC=90°，若AD⊥PB，垂足为D，求证：AD⊥面BPC．

Answer 1

分析 先证明PA⊥BC，从而证明BC⊥平面PAB，得出BC⊥AD，从而证明AD⊥平面BPC．

解答 解：三棱锥P-ABC中，PA⊥面ABC，BC?平面ABC，∴PA⊥BC；
又∠ABC=90°，∴AB⊥BC，
又PA∩AB=A，PA?平面PAB，AB?平面PAB，
∴BC⊥平面PAB；
又AD?平面PAB，
∴BC⊥AD；
又AD⊥PB，且BC∩PB=B，
BC?平面PBC，PB?平面PBC，
∴AD⊥平面BPC．

点评 本题考查了空间中的垂直关系的应用问题，也考查了推理与证明的应用问题，是中档题目．