题目内容
13.已知数列{an}的通项公式为an=n2+kn+5,若对于任意的正整数n,都有an+1>an,则实数K的范围为k>-3.分析 由于对于任意的正整数n,都有an+1>an,代入可得(n+1)2+k(n+1)+5>n2+kn+5,化简利用数列的单调性即可得出.
解答 解:∵对于任意的正整数n,都有an+1>an,
∴(n+1)2+k(n+1)+5>n2+kn+5,
化为k>-(2n+1),
由于数列{-(2n+1)}单调递减,
∴-(2n+1)≤-3.
∴k>-3,
故答案为:k>-3.
点评 本题考查了数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.函数f(x)=ex+x-2的零点所在的区间是(e≈2.71828)( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
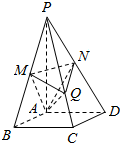 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.