题目内容
11.已知函数f(x)=ax2-bx+1.(1)求实数a,b使不等式f(x)<0的解集是{x|3<x<4};
(2)若a为整数,b=a+2,且函数f(x)在(-2,-1)上恰有一个零点,求a的值.
分析 (1)利用不等式ax2-bx+1<0的解集是{x|3<x<4},推出方程ax2-bx+1=0的两根是3和4,求解即可.
(2)利用已知条件推出f(-2)•f(-1)<0,求出a的范围,然后求解即可.
解答 解:(1)∵不等式ax2-bx+1<0的解集是{x|3<x<4},
∴方程ax2-bx+1=0的两根是3和4,….(2分)
∴解得a=$\frac{1}{12}$,b=$\frac{7}{12}$.….(6分)
(2)∵b=a+2,∴f(x)=ax2-(a+2)x+1.….(7分)
∵△=(a+2)2-4a=a2+4>0,
∴函数f(x)=ax2-bx+1必有两个零点.….(8分)
又函数f(x)在(-2,-1)上恰有一个零点,
∴f(-2)•f(-1)<0,∴(6a+5)(2a+3)<0,….(10分)
解得-$\frac{3}{2}$<a<-$\frac{5}{6}$.∵a∈Z,∴a=-1.….(12分)
点评 本题考查二次表达式的解法,函数的零点与方程根的关系,考查计算能力.

练习册系列答案
相关题目
16.已知点C在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,以C为圆心的圆与x轴相切于椭圆的右焦点F,若圆C与y轴相切,则椭圆的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{3}$-1 |
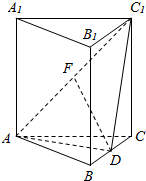 如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.