题目内容
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A.2 | B.3 | C.6 | D.9 |
D
解析试题分析: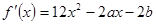 ,
,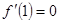 ,
,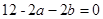 ,
,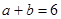 ,所以
,所以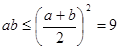 .故选D.
.故选D.
考点:函数极值的应用

练习册系列答案
相关题目
函数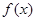 的导函数
的导函数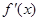 的图像如图所示,则( )
的图像如图所示,则( )
A.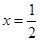 为 为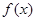 的极大值点 的极大值点 | B.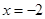 为 为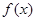 的极大值点 的极大值点 |
C.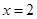 为 为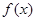 的极大值点 的极大值点 | D.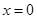 为 为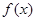 的极小值点 的极小值点 |
已知函数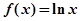 ,
,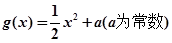 ,直线
,直线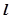 与 函数
与 函数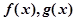 的图像都相切,且
的图像都相切,且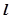 与函数
与函数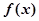 图像的切点的横坐标为1,则
图像的切点的横坐标为1,则 的值为 ( )
的值为 ( )
| A.1 | B.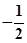 | C.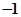 | D.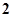 |
函数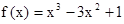 是减函数的区间为 ( )
是减函数的区间为 ( )
A.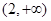 | B.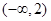 | C.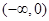 | D.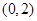 |
函数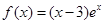 的单调递增区间是 ( )
的单调递增区间是 ( )
A.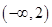 | B.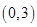 | C.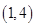 | D.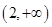 |
已知函数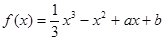 ,
,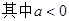 ,如果存在实数
,如果存在实数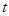 ,使
,使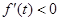 ,则
,则 的值( )
的值( )
| A.必为正数 | B.必为负数 | C.必为非负 | D.必为非正 |
设函数f(x)满足x2f′(x)+2xf(x)=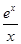 ,f(2)=
,f(2)=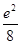 ,则x>0时,f(x)( )
,则x>0时,f(x)( )
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
函数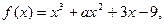 已知
已知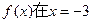 时取得极值,则
时取得极值,则 的值等于( )
的值等于( )
| A.2 | B.3 | C.4 | D.5 |
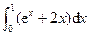 =( )
=( )
| A.1 |
B.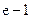 |
| C.e |
| D.1+e |