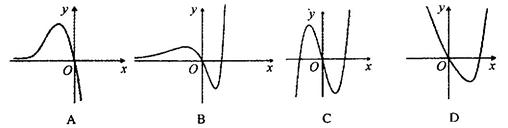
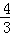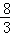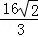题目内容
已知函数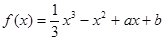 ,
,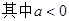 ,如果存在实数
,如果存在实数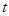 ,使
,使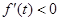 ,则
,则 的值( )
的值( )
| A.必为正数 | B.必为负数 | C.必为非负 | D.必为非正 |
A
解析试题分析:∵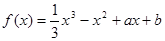 ,∴f′(x)=x2-2x+a.∵存在实数t,使f'(t)<0,a>0,∴t2-2t+a<0的解集不是空集,∴△=4-4a>0,解得a<1,因此0<a<1.令t2-2t+a=0,解得t=1±
,∴f′(x)=x2-2x+a.∵存在实数t,使f'(t)<0,a>0,∴t2-2t+a<0的解集不是空集,∴△=4-4a>0,解得a<1,因此0<a<1.令t2-2t+a=0,解得t=1±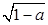 ,∴t2-2t+a<0的解集是{x|0<1?
,∴t2-2t+a<0的解集是{x|0<1?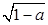 <t<1+
<t<1+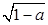 <2}.∵f′(2-t)=(2-t)2-2(2-t)+a=t(t-2)+a,∴f′(2-t)<0;∵
<2}.∵f′(2-t)=(2-t)2-2(2-t)+a=t(t-2)+a,∴f′(2-t)<0;∵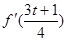 =(
=(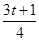 )2?2×
)2?2×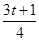 +a=
+a=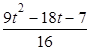 +a,∴f′(t)?f′(
+a,∴f′(t)?f′(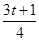 )=t2?2t?
)=t2?2t?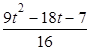 =
=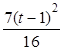 ≥0,∴f′(
≥0,∴f′(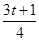 )≤f′(t)<0,∴f′(t+2)•f′(
)≤f′(t)<0,∴f′(t+2)•f′(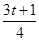 )>0,故选A.
)>0,故选A.
考点:导数的运算.

练习册系列答案
相关题目
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A.2 | B.3 | C.6 | D.9 |
函数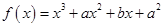 在
在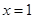 时有极值10,则
时有极值10,则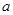 的值为( )
的值为( )
| A.-3或4 | B.4 | C.-3 | D.3或 4 |
设函数f(x)=x-2msin x+(2m-1)sin xcos x(m为实数)在(0,π)上为增函数,则m的取值范围为( )
A.[0,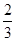 ] ] | B.(0,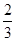 ) ) | C.(0,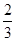 ] ] | D.[0,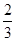 ) ) |
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )
A.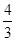 | B.2 | C.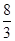 | D. |
已知函数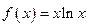 .若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
.若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
| A.x+y-1=0 |
| B.x-y-1=0 |
| C.x+y+1=0 |
| D.x-y+1=0 |
已知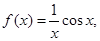 则
则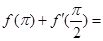 ( )
( )
A.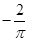 |
B. |
C.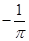 |
D.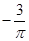 |
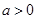 时,函数
时,函数 的图象大致是
的图象大致是