题目内容
1.已知sin(5π-α)=$\sqrt{2}$cos($\frac{π}{2}$-β)和$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),且0<α<π,0<β<π,求α和β的值.分析 利用三角函数的诱导公式进行化简即可.
解答 解:∵sin(5π-α)=$\sqrt{2}$cos($\frac{π}{2}$-β)和$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),
∴sinα=$\sqrt{2}$sinβ和$\sqrt{3}$cosα=$\sqrt{2}$cosβ,
两式平方相加得sin2α+3cos2α=2,
即2cos2α=1,cos2α=$\frac{1}{2}$,
∴cosα=±$\frac{\sqrt{2}}{2}$,
∵0<α<π,∴α=$\frac{π}{4}$或$\frac{3π}{4}$,
当α=$\frac{π}{4}$时,$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$cosβ,即cosβ=$\frac{\sqrt{3}}{2}$,则β=$\frac{π}{6}$.
当α=$\frac{3π}{4}$时,$\sqrt{3}$×(-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$cosβ,即cosβ=-$\frac{\sqrt{3}}{2}$,则β=$\frac{5π}{6}$.
点评 本题主要考查三角函数值的求解,利用两角和差的正弦和余弦公式,以及同角的三角函数关系是解决本题的关键.

练习册系列答案
相关题目
16.已知△ABC的三个顶点在以O为球心的球面上,且cosC=$\frac{1}{3}$,BC=1,AC=3,三棱锥O-ABC的体积为$\frac{\sqrt{14}}{6}$,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 24π |
12.设抛物线C:y=x2与直线l:y=1围成的封闭图形记为P,则图形P的面积S等于( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
8.复数z=$\frac{{{{(1+i)}^2}}}{1-i}$的共轭复数$\overline{z}$=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
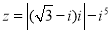 (
( 为虚数单位),则复数
为虚数单位),则复数 的共轭复数为( )
的共轭复数为( ) 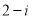 B.
B. C.
C.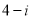 D.
D.
 已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.
已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.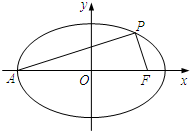 如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A,右焦点为F(c,0).P(x0,y0)为椭圆上一点,且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A,右焦点为F(c,0).P(x0,y0)为椭圆上一点,且PA⊥PF.