题目内容
16.已知△ABC的三个顶点在以O为球心的球面上,且cosC=$\frac{1}{3}$,BC=1,AC=3,三棱锥O-ABC的体积为$\frac{\sqrt{14}}{6}$,则球O的表面积为( )| A. | 4π | B. | 8π | C. | 16π | D. | 24π |
分析 通由余弦定理可知AB,求出B的大小,利用三棱锥O-ABC的体积为$\frac{\sqrt{14}}{6}$,求出O到底面的距离,求出球的半径,然后求出球的表面积.
解答 解:∵△ABC,cosC=$\frac{1}{3}$,BC=1,AC=3,
∴由余弦定理可知:AB=$\sqrt{1+9-2×1×3×\frac{1}{3}}$=2$\sqrt{2}$,
∴AB2+BC2=AC2,
∴B=90°.
∴斜边AC的中点就是△ABC的外接圆的圆心,
设三棱锥O-ABC的底面ABC上的高为h,则
∵三棱锥O-ABC的体积为$\frac{\sqrt{14}}{6}$,
∴$\frac{1}{3}×2\sqrt{2}×1×h$×$\frac{1}{2}$=$\frac{\sqrt{14}}{6}$,
∴h=$\frac{\sqrt{7}}{2}$,ABC的外接圆的半径为$\frac{1}{2}$•$\frac{2\sqrt{2}}{\frac{2\sqrt{2}}{3}}$=$\frac{3}{2}$,
∴R=$\sqrt{\frac{7}{4}+\frac{9}{4}}$=2,
球O的表面积为4πR2=16π.
故选:C.
点评 本题考查球的表面积的求法,球的内含体与三棱锥的关系,考查空间想象能力以及计算能力.

 天天练口算系列答案
天天练口算系列答案某市乘坐出租车的收费办法如下:
⑴不超过4千米的里程收费12元; ⑵超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费); 当车程超过4千米时,另收燃油附加费1元. |
相应系统收费的程序框图如图所示,其中 (单位:千米)为行驶里程,
(单位:千米)为行驶里程, (单位:元)为所收费用,用
(单位:元)为所收费用,用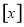 表示不大于
表示不大于 的最大整数,则图中①处应填( )
的最大整数,则图中①处应填( )

A.  B.
B.  C.
C.  D.
D. 
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |