题目内容
12. 已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.
已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.(Ⅰ)求抛物线C2的方程;
(Ⅱ)过点F的直线交抛物线C1于点A(x1,y1),B(x2,y2)(x1<x2),过A,B分别作C1的切线l1,l2交于点P,记直线l1,l2与C2的交点为M(m1,n1),N(m2,n2)(m1<m2),问:是否存在直线AB,使得$\frac{{S}_{△APB}}{{S}_{△PMN}}$=2(3+2$\sqrt{2}$)?若存在,求出满足条件的直线AB的方程;若不存在,请说明理由.
分析 (I)设抛物线C1的标准方程为:x2=2py(p>0),把点(2,1)代入解得p,即可得出;即可得出抛物线C2的方程为x2=-2py.
(II)假设存在直线AB,使得$\frac{{S}_{△APB}}{{S}_{△PMN}}$=2(3+2$\sqrt{2}$).设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+1.与抛物线方程联立可得x2-4kx-4=0,得到根与系数的关系.由${y}^{′}=\frac{1}{2}x$,可得切线AP的方程为:$y-\frac{{x}_{1}^{2}}{4}=\frac{1}{2}{x}_{1}(x-{x}_{1})$,化为$y=\frac{1}{2}{x}_{1}x-\frac{{x}_{1}^{2}}{4}$,同理可得BP的方程:$y=\frac{1}{2}{x}_{2}x$-$\frac{{x}_{2}^{2}}{4}$.联立可得P(2k,-1).把切线方程与x2=-4y联立解得xM=$(\sqrt{2}-1){x}_{1}$,同理可得${x}_{N}=(\sqrt{2}-1){x}_{2}$.利用$\frac{{S}_{△APB}}{{S}_{△PMN}}$=$\frac{|PA||PB|}{|PM||PN|}$=$\frac{({x}_{P}-{x}_{1})({x}_{2}-{x}_{P})}{({x}_{P}-{x}_{M})({x}_{N}-{x}_{P})}$.代入解出即可.
解答 解:(I)设抛物线C1的标准方程为:x2=2py(p>0),
把点(2,1)代入可得:4=2p,解得p=2,
∴抛物线C1的标准方程为x2=4y.
∵抛物线C2与C1关于x轴对称,
∴抛物线C2的方程为x2=-4y.
(II)假设存在直线AB,使得$\frac{{S}_{△APB}}{{S}_{△PMN}}$=2(3+2$\sqrt{2}$).
设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+1.
联立$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$,化为x2-4kx-4=0,
∴x1+x2=4k,x1x2=-4.
由${y}^{′}=\frac{1}{2}x$,
则切线AP的方程为:$y-\frac{{x}_{1}^{2}}{4}=\frac{1}{2}{x}_{1}(x-{x}_{1})$,化为$y=\frac{1}{2}{x}_{1}x-\frac{{x}_{1}^{2}}{4}$,
同理可得BP的方程:$y=\frac{1}{2}{x}_{2}x$-$\frac{{x}_{2}^{2}}{4}$.
联立$\left\{\begin{array}{l}{y=\frac{1}{2}{x}_{1}x-\frac{{x}_{1}^{2}}{4}}\\{y=\frac{1}{2}{x}_{2}x-\frac{{x}_{2}^{2}}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}=2k}\\{y=\frac{{x}_{1}{x}_{2}}{4}=-1}\end{array}\right.$,∴P(2k,-1).
联立$\left\{\begin{array}{l}{y=\frac{1}{2}{x}_{1}x-\frac{{x}_{1}^{2}}{4}}\\{{x}^{2}=-4y}\end{array}\right.$,化为${x}^{2}+2{x}_{1}x-{x}_{1}^{2}$=0,
解得xM=$(\sqrt{2}-1){x}_{1}$,
同理可得${x}_{N}=(\sqrt{2}-1){x}_{2}$.
$\frac{{S}_{△APB}}{{S}_{△PMN}}$=$\frac{|PA||PB|}{|PM||PN|}$=$\frac{({x}_{P}-{x}_{1})({x}_{2}-{x}_{P})}{({x}_{P}-{x}_{M})({x}_{N}-{x}_{P})}$.
分子=${x}_{P}({x}_{1}+{x}_{2})-{x}_{P}^{2}-{x}_{1}{x}_{2}$=2k•4k-4k2+4=4(k2+1).
分母=${x}_{P}({x}_{M}+{x}_{N})-{x}_{P}^{2}-{x}_{M}{x}_{N}$=${x}_{P}(\sqrt{2}-1)({x}_{1}+{x}_{2})$-${x}_{P}^{2}$-$(3-2\sqrt{2}){x}_{1}{x}_{2}$=$8{k}^{2}(\sqrt{2}-1)-4{k}^{2}-(3-2\sqrt{2})×(-4)$=$4(3-2\sqrt{2})(1-{k}^{2})$,
∴$\frac{4(1+{k}^{2})}{4(3-2\sqrt{2})(1-{k}^{2})}$=$2(3+2\sqrt{2})$,
化为3k2=1,解得k=$±\frac{\sqrt{3}}{3}$.
因此存在直线AB:$y=±\frac{\sqrt{3}}{3}x+1$,使得$\frac{{S}_{△APB}}{{S}_{△PMN}}$=2(3+2$\sqrt{2}$).
点评 本题考查了抛物线的定义标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、利用导数的几何意义可得切线的斜率、三角形的面积之比,考查了推理能力与计算能力,属于难题.

| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
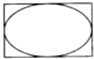 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A. | 17.84 | B. | 18.84 | C. | 5.16 | D. | 6.16 |
 ,则下列不等式错误的是( )
,则下列不等式错误的是( ) B.
B.
 D.
D.
 分别与曲线
分别与曲线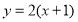 ,
, 交于A,B,则
交于A,B,则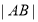 的最小值为( )
的最小值为( ) D.
D.
 的顶点都在抛物线
的顶点都在抛物线 上,且
上,且 ,则点
,则点 到抛物线的焦点的距离是_____________.
到抛物线的焦点的距离是_____________.