题目内容
已知函数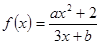 是奇函数,且
是奇函数,且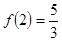 .
.
(1)求实数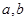 的值;
的值;
(2)判断函数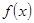 在
在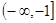 上的单调性,并用定义加以证明.
上的单调性,并用定义加以证明.
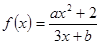 是奇函数,且
是奇函数,且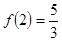 .
.(1)求实数
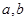 的值;
的值;(2)判断函数
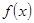 在
在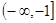 上的单调性,并用定义加以证明.
上的单调性,并用定义加以证明.(1)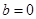 ,
,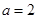 ;(2)
;(2)  在
在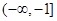 上为增函数
上为增函数
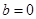 ,
,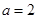 ;(2)
;(2)  在
在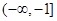 上为增函数
上为增函数试题分析:(1)由题意函数
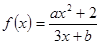 是奇函数可得
是奇函数可得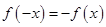 ,从而对应项相等可求得
,从而对应项相等可求得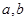 ;
;(2)由函数单调性的定义判断即可.任取
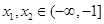 ,设
,设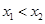 ,作差
,作差 后化积,判断符号即可.
后化积,判断符号即可.试题解析:(1) 由题意函数
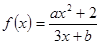 是奇函数可得
是奇函数可得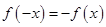
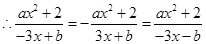
因此
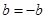 ,即
,即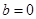 ,
,又
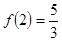
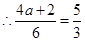 即
即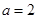
(2)由(1)知
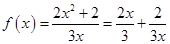 ,
, 在
在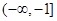 上为增函数
上为增函数证明:设
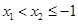 ,则
,则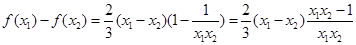
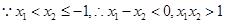
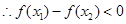 即
即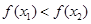
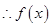 在
在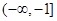 上为增函数
上为增函数
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
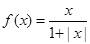 ,甲、乙、丙三位同学在研究此函数的性质时分别给出下列命题:
,甲、乙、丙三位同学在研究此函数的性质时分别给出下列命题: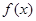 为偶函数;
为偶函数; ;
; 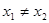 则一定有
则一定有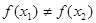
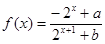 (
(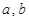 为实常数).
为实常数).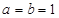 时,证明:
时,证明: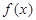 不是奇函数;②
不是奇函数;②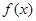 是
是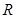 上的单调递减函数.
上的单调递减函数.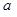 与
与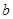 的值.
的值.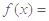
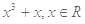 ,当
,当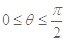 时,
时,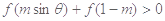 恒成立,则实数
恒成立,则实数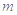 的取值范围是( )
的取值范围是( )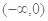
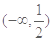
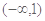
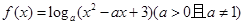 满足:对任意实数
满足:对任意实数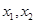 ,当
,当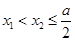 时,总有
时,总有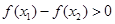 ,则实数
,则实数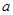 的取值范围是( )
的取值范围是( )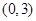
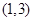
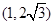
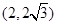
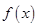 是
是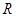 上的减函数,且
上的减函数,且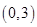 和
和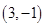 ,则不等式
,则不等式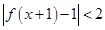 的解集是( )
的解集是( )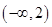
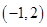
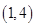
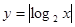 的单调递减区间是 .
的单调递减区间是 .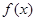 在区间
在区间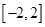 上单调递减,则不等式
上单调递减,则不等式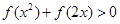 的解集是( )
的解集是( )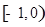
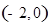
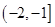

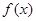 是
是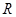 上增函数,若
上增函数,若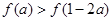 ,则a的取值范围是
,则a的取值范围是