Question

【题目】函数f（x）= ．
（1）若a=5，求函数f（x）的定义域A；
（2）设B={x|﹣1＜x＜2}，当实数a，b∈B∩（RA）时，求证： ＜|1+ |．

Answer 1

【答案】
（1）

解： a=5时，函数f（x）= ，

∴|x+1|+|x+2|﹣5≥0；

即|x+1|+|x+2|≥5，

当x≥﹣1时，x+1+x+2≥5，∴x≥1；

当﹣1＞x＞﹣2时，﹣x﹣1+x+2≥5，∴x∈；

当x≤﹣2时，﹣x﹣1﹣x﹣2≥5，∴x≤﹣4；

综上，f（x）的定义域是A={x|x≤﹣4或x≥1}．

（2）

证明：∵A={x|x≤﹣4或x≥1}，B={x|﹣1＜x＜2}，

∴RA=（﹣4，1），

∴B∩CRA=（﹣1，1）；

又∵ ，

而 ；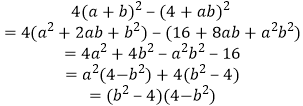

当a，b∈（﹣1，1）时，

（b2﹣4）（4﹣a2）＜0

∴4（a+b）2＜（4+ab）2，

即 ．

【解析】（1）根据题意，得|x+1|+|x+2|﹣5≥0；求出x的取值范围，即是f（x）的定义域A；（2）由A、B求出B∩CRA，即得a、b的取值范围，由此证明 成立即可．
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识，掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零，以及对不等式的证明的理解，了解不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．