题目内容
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
(I)求该班学生参加活动的人均次数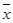 ;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率
;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率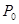 .
.
(III)从该班中任选两名学生,用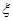 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量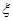 的分布列及数学期望
的分布列及数学期望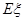 .
.
(1)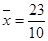 ;(2)
;(2) ;(3)
;(3)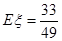 .
.
解析试题分析:(1)根据图形能够知道参加活动1次、2次和3次的学生人数,人均次数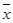 的计算需要注意参加2次活动的要乘以2,如
的计算需要注意参加2次活动的要乘以2,如 ;(2)“参加活动次数恰好相等”的事件有
;(2)“参加活动次数恰好相等”的事件有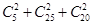 ,任选两名学生有
,任选两名学生有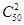 ,则最后
,则最后 ;(3)由题意该班中任选两名学生的情况有“这两人中一人参加1次活动,另一人参加2次活动”,“这两人中一人参加2次活动,另一人参加3次活动”,“这两人中一人参加1次活动,另一人参加3次活动”,
;(3)由题意该班中任选两名学生的情况有“这两人中一人参加1次活动,另一人参加2次活动”,“这两人中一人参加2次活动,另一人参加3次活动”,“这两人中一人参加1次活动,另一人参加3次活动”,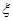 的取值有0,1,2,其概率分别为
的取值有0,1,2,其概率分别为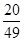 ,
,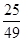 ,
,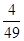 ,进而可以求出
,进而可以求出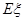 .
.
试题解析:由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.
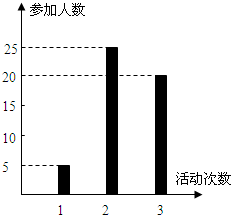
(I)该班学生参加活动的人均次数为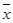 =
=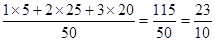 .
.
(II)从该班中任选两名学生,他们参加活动次数恰好相等的概率为 .
.
(III)从该班中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件 ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件 ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件 .易知
.易知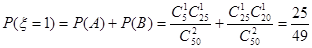 ;
; 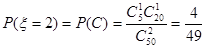 .
. 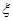 的分布列:
的分布列: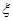
0 1 2 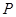
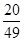
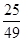
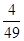
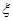 的数学期望:
的数学期望: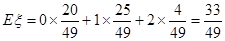 .
.
考点:1.平均数的求解,2.古典概型,期望.

(12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生
(I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.

某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 |
| 温差(℃) | 9 | 10 | 8 | 11 |
| 发芽数(粒) | 33 | 39 | 26 | 46 |
(2)若研究的一个项目在这四天中任选2天的种子发芽数来进行,记发芽的种子数分别为m,n(m<n),则以(m,n)的形式列出所有的基本事件,并求“m,n满足
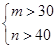 ”的事件A的概率.
”的事件A的概率.  位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为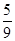 .
.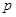 的值;
的值;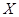 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量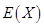 .
.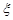 的分布列和数学期望.
的分布列和数学期望. 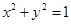 相切的概率;
相切的概率;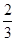 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.