题目内容
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 、
、![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有两个不同零点,求实数
上有且只有两个不同零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() 的单调增区间为
的单调增区间为![]() ;
;
(2)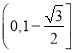 .
.
【解析】
(1)由周期可求出![]() ,再将点
,再将点![]() 代入可求出
代入可求出![]() ,从而可得函数
,从而可得函数![]() 的解析式,再整体代入法即可求出函数的单调增区间;
的解析式,再整体代入法即可求出函数的单调增区间;
(2)由题意得![]() ,由
,由![]() 得方程
得方程![]() 在区间
在区间![]() 上有且只有两个不同的实数根,结合图象,根据函数的值域即可求出答案.
上有且只有两个不同的实数根,结合图象,根据函数的值域即可求出答案.
解:(1)∵函数![]() 的最小正周期为
的最小正周期为![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又函数![]() 的图象过点
的图象过点![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() 得
得![]() ,
,
综上:![]() ,
,![]() ,
,![]() 的单调增区间为
的单调增区间为![]() ;
;
(2)由题意得![]() ,
,
由![]() 得
得![]() ,
,
由题意可得函数![]() 的图象和函数
的图象和函数![]() 的图象在区间
的图象在区间![]() 上有且只有两个不同的交点,
上有且只有两个不同的交点,

由图可知,![]() ,
,![]() ,
,
∴ ,
,
故实数![]() 的取值范围是
的取值范围是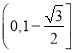 .
.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目