Question

（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（不等式选做题）不等式|

x+1

x-1

|≥1的解集是

（-∞，0]

．
B．（几何证明选做题） 如图，以AB=4为直径的圆与△ABC的两边分别交于E，F两点，∠ACB=60°，则EF=

2

．
C．（坐标系与参数方程选做题） 在极坐标中，已知点P为方程ρ（cosθ+sinθ）=1所表示的曲线上一动点，Q（2，

π

3

），则|PQ|的最小值为

6

2

．

Answer 1

分析：A 由不等式|

x+1

x-1

|≥1可得

|x-1|≥|x+1| x-1≠0

，由此求出不等式的解集．
B 由题意得CA=2CE，再由圆内接四边形性质可得∠CFE=∠CBA，∠C=∠C，故有△CEF∽△CBA，对应边成比列，从而求出EF 的值．
C  点P为方程化为直角坐标方程，把点的极坐标化为直角坐标，|PQ|的最小值为点Q到直线的距离d，由点到直线的距离公式求得d的值．

解答：解：A 由不等式|

x+1

x-1

|≥1可得

|x-1|≥|x+1| x-1≠0

，
即

(x-1)2≥(x+1)2 x≠1

，解得 x≤0．
故答案为 （-∞，0]．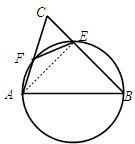
B  如图，连接AE，∵AB为圆的直径，∴∠AEB=∠AEC=90°．
又∵∠ACB=60°，∴CA=2CE，由圆内接四边形性质易得：
∠CFE=∠CBA （由圆内接四边形对角互补，同角的补角相等得到的）．
又因为∠C=∠C，△CEF∽△CAB，∴

EF

BA

=

CE

CA

=

1

2

，
又∵AB=4，∴EF=2．
故答案为 2．
C  点P为方程ρ（cosθ+sinθ）=1 即 x+y-1=0，表示一条直线，Q（2，

π

3

）的直角坐标为（1，

3

），
故|PQ|的最小值为点Q到直线的距离d，
d=

|1+ 3 -1|

2

=

6

2

，
故答案为

6

2

．

点评：本题主要考查绝对值不等式的解法，圆内接四边形的性质、相似三角形的性质，把极坐标方程化为直角坐标方程的方法，属于中档题．