题目内容
函数y=sin2x的图象向右平移φ（φ＞0）个单位，得到的图象恰好关于x=
对称，则φ的最小值为（ ）
| π |
| 6 |
分析：令y=f（x）=sin2x，依题意f（x-φ）=sin2（x-φ）关于x=
对称，从而可求得φ的最小值．
| π |
| 6 |
解答：解：令y=f（x）=sin2x，
则f（x-φ）=sin2（x-φ）=sin（2x-2φ），且其图象恰好关于x=
对称，
∴2×
-2φ=2kπ+
或2×
-2φ=2kπ-
，k∈Z．
∴φ=-kπ-
或φ=-kπ+
，k∈Z．
又φ＞0，
∴φ的最小值为
．
故选A．
则f（x-φ）=sin2（x-φ）=sin（2x-2φ），且其图象恰好关于x=
| π |
| 6 |
∴2×
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴φ=-kπ-
| π |
| 12 |
| 5π |
| 12 |
又φ＞0，
∴φ的最小值为
| 5π |
| 12 |
故选A．
点评：本题考查y=Asin（ωx+φ）的部分图象变换，考查正弦函数的对称性质，属于中档题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
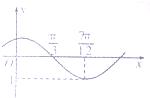（2013•蚌埠二模）已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜