题目内容
（2013•蚌埠二模）已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π | 2 |
（I） 求函数f（x）的解析式；
（II）如何通过变换函数f（x）的图象得到函数y=sin2x的图象？
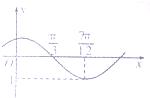
分析：（I）利用图象的最低点确定A的值，利用周期确定ω，再根据图象过点（
，0），确定φ的值，即可求函数f（x）的解析式；
（II）f（x）=sin（2x+
）=sin[2（x+
）]，由此可得结论．
| π |
| 3 |
（II）f（x）=sin（2x+
| π |
| 3 |
| π |
| 6 |
解答：解：（I）由题意，函数的最小值为-1，∴A=1，
∵T=4×（
π-
）=π，
∴ω=2，
∴f（x）=sin（2x+φ），
∵图象过点（
，0），
∴sin（2×
+φ）=0，
∵|φ|＜
，∴φ=
∴f（x）=sin（2x+
）；
（II）∵f（x）=sin（2x+
）=sin[2（x+
）]
∴函数f（x）的图象向右平移
个单位长度，可以得到函数y=sin2x的图象．
∵T=4×（
| 7 |
| 12 |
| π |
| 3 |
∴ω=2，
∴f（x）=sin（2x+φ），
∵图象过点（
| π |
| 3 |
∴sin（2×
| π |
| 3 |
∵|φ|＜
| π |
| 2 |
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
（II）∵f（x）=sin（2x+
| π |
| 3 |
| π |
| 6 |
∴函数f（x）的图象向右平移
| π |
| 6 |
点评：本题考查三角函数解析式的确定，考查图象的变换，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目