题目内容
【题目】如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A.风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为（ ）
A. 5米B. (4＋
)米
C. (4＋
)米D. (4＋
)米
【答案】D
【解析】
以圆心
为原点，以水平方向为
轴方向，以竖直方向为
轴方向建立平面直角坐标系，则根据大风车的半径为
，圆上最低点
离地面1米，
秒转动一圈，可得到
与
间的函数关系式，求出
的坐标，即可求出点到点
的距离与点的高度之和.
以圆心为原点，以水平方向为x轴方向，以竖直方向为y轴方向，
建立平面直角坐标系，如图所示．
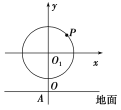
设∠OP＝θ，运动t(秒)后与地面的距离为f(t)，又T＝12，
∴θ＝
t，∴f(t)＝3－2cos t，t≥0，
风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，
θ＝6π＋
，P(
，1)，
∴点P的高度为3－2×
＝4.∵A(0，－3)，∴AP＝
＝
，
∴点P到点A的距离与点P的高度之和为(4＋)米，故选D．
【题目】汽车制造商在2019年年初公告：公司计划2019年的生产目标为43万辆.已知该公司近三年的汽车生产量如表所示：
年份(年） | 2016 | 2017 | 2018 |
产量（万辆） | 8 | 18 | 30 |
如果我们分别将2016，2017，2018，2019定义为第一、二、三、四年.现在有两个函数模型：二次函数模型
，指数型函数模型
，哪个模型能更好地反映该公司年产量y与年份x的关系？
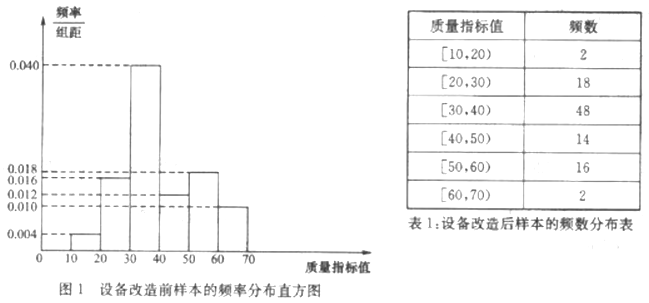
【题目】某企业对现有设备进行了改造，为了了解设备改造后的效果，现从设备改造前后生产的大量产品中各抽取了100件产品作为样本，检测其质量指标值，若质量指标值在
内，则该产品视为合格品，否则视为不合格品．图1是设备改造前的样本的频率分布直方图，表1是设备改造后的样本的频数分布表．
（1）完成
列联表，并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关：
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（2）根据图1和表1提供的数据，试从产品合格率的角度对改造前后设备的优劣进行比较；
（3）企业将不合格品全部销毁后，根据客户需求对合格品进行等级细分，质量指标值落在
内的定为一等品，每件售价180元；质量指标值落在
或
内的定为二等品，每件售价150元；其他的合格品定为三等品，每件售价120元．根据频数分布表1的数据，用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率．现有一名顾客随机购买两件产品，设其支付的费用为
（单位：元），求的分布列和数学期望．
附：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
