题目内容
已知向量 ,
, ,若函数
,若函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若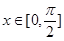 ,求
,求 的最大值及相应的
的最大值及相应的 值;
值;
(3)若 ,求
,求 的单调递减区间.
的单调递减区间.
(1) ;(2)
;(2)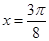 ,
,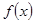 有最大值
有最大值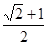 ,(3)
,(3)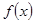 的单调减区间
的单调减区间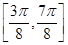 .
.
解析试题分析:(1)利用两角和正弦公式和降幂公式化简,得到 的形式,利用公式
的形式,利用公式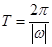 计算周期.(2)利用正弦函数的单调区间,求在
计算周期.(2)利用正弦函数的单调区间,求在 的单调性.(3)求三角函数的最小正周期一般化成
的单调性.(3)求三角函数的最小正周期一般化成 ,
,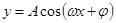 ,
,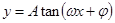 形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成
形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成 形式,再
形式,再 的单调区间,只需把
的单调区间,只需把 看作一个整体代入
看作一个整体代入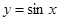 相应的单调区间,注意先把
相应的单调区间,注意先把 化为正数,这是容易出错的地方.
化为正数,这是容易出错的地方.
试题解析:解: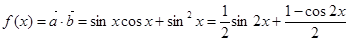 =
=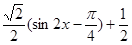
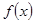 的最小正周期为
的最小正周期为
当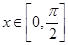 时,
时,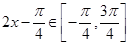 ,当
,当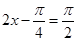 ,即
,即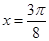 时,
时,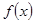 有最大值
有最大值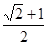
当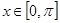 时,
时,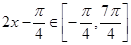 ,由
,由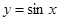 的图像知,
的图像知,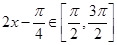 ,
,
即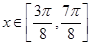 时,
时,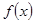 单调递减.
单调递减.
所以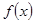 的单调减区间
的单调减区间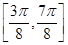
考点:(1)三角函数的周期性;(2)三角函数的最值;(3)三角函数的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合; 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到? 的一系列对应值如下表:
的一系列对应值如下表:










 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,
时, 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.  在一个周期内,当
在一个周期内,当 时,
时, 取得最小值
取得最小值 ;当
;当 时,
时,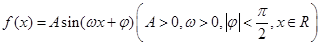 图象的一部分如图所示.
图象的一部分如图所示. 的解析式;
的解析式; 时,求函数
时,求函数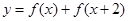 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.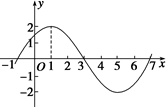
 ,且
,且 ∥
∥ .
. ;
;  .
.
 时,
时, 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.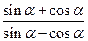 +cos2α=_____________.
+cos2α=_____________.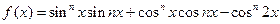 ,对任意
,对任意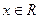 都使
都使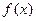 为常数,则正整数
为常数,则正整数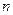 为________
为________