题目内容
已知函数
(1)当函数 取得最大值时,求自变量
取得最大值时,求自变量 的集合;
的集合;
(2)该函数的图象可由 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(1)当y取得最大值时,x的集合为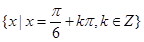 ,(2)略.
,(2)略.
解析试题分析:(1)欲求函数最值,需将函数化为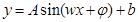 的形式,首先应将三角函数的次数化为一次,利用
的形式,首先应将三角函数的次数化为一次,利用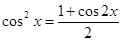 ,
,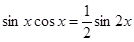 ,代入并配角合并;(2)函数的平移要注意方向和平移的量,并注意平移是针对变量而言的,伸缩也是针对变量而言,即在变量上变化.
,代入并配角合并;(2)函数的平移要注意方向和平移的量,并注意平移是针对变量而言的,伸缩也是针对变量而言,即在变量上变化.
试题解析:
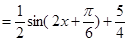 2分
2分
当y取得最大值时,必需且只需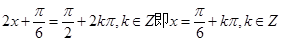
当y取得最大值时,x的集合为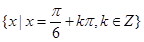 6分
6分
(2)将函数y=sinx的图象依次进行如下变换:
1)把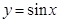 的图象向左平移
的图象向左平移 ,得
,得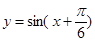 图象.
图象.
2)把所得图象上的各点横坐标缩到原来的 (纵坐标不变)
(纵坐标不变)
得到函数 的图象 10分
的图象 10分
3)把所得图象上的各点纵坐标缩到原来的 (横坐标不变)
(横坐标不变)
得到函数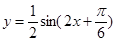 的图象
的图象
4)把图象上移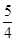 个大内长度,得
个大内长度,得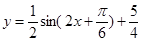 图象
图象
综上得到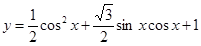 的图象 14分
的图象 14分
考点:(1)三角函数最值;(2)三角函数平移和伸缩变化.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
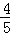 ,α为第三象限角.
,α为第三象限角.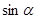 ,
, 的值;
的值;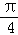 ),tan2α的值.
),tan2α的值.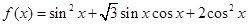 .
. 的最小正周期;
的最小正周期; ,
, ,若函数
,若函数 .
.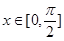 ,求
,求 值;
值; ,求
,求 <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,- ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 .
. 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围. 中,内角
中,内角 所对边长分别为
所对边长分别为 ,
, ,
,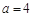 .
. 的最大值及
的最大值及 的取值范围;
的取值范围; 的值域.
的值域.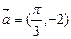 平移后,得到的图象的表达式为
平移后,得到的图象的表达式为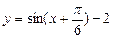 ,则原函数的解析式为
,则原函数的解析式为 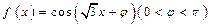 .若
.若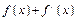 是奇函数,则
是奇函数,则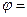 __________.
__________.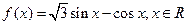 ,若
,若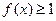 ,
, 则x的取值范围为
则x的取值范围为