题目内容
(12分)
已知数列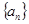 中,
中,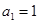 ,且当
,且当 时,函数
时,函数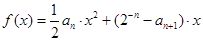
取得极值;
(Ⅰ)若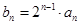 ,证明数列
,证明数列 为等差数列;
为等差数列;
(Ⅱ)设数列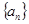 的前
的前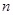 项和为
项和为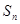 ,求
,求 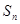 .
.
【答案】
(1)略
(2) 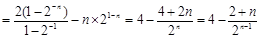
【解析】解:(Ⅰ) ……1分
……1分
由题意 得
得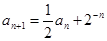 由
由
得 ……4分
……4分
又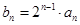
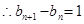 ,所以数列
,所以数列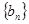 是首项为
是首项为 、
、
公差为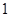 的等差数列 所以
的等差数列 所以 ……6分
……6分
(Ⅱ) 由(1)可得  ……7分
……7分

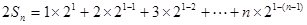
两式相减得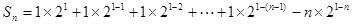 ……10分
……10分
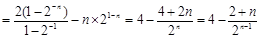 ……12分
……12分

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
 中a1=2,点
中a1=2,点 在函数
在函数 的图象上,
的图象上,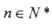 .数列
.数列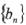 的前n项和为Sn,且满足b1=1,当n
的前n项和为Sn,且满足b1=1,当n 2时,
2时, .
. 是等比数列;
是等比数列; 求
求 的值.
的值.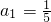 ,且当n>1,n∈N*时,有
,且当n>1,n∈N*时,有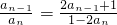 ,
, 为等差数列;
为等差数列;