题目内容
(14分)已知数列
中，
当
且
有：
。
(Ⅰ)设数列
满足
，证明散列
为等比数列，并求数列的通项公式；
(Ⅱ)记
，规定
，求数列
的前
项和
。
解析：(Ⅰ)由已知条件，得
则
……………………(2分)
即
∴
∵
∴
是首项为
，公比为
的等比数列 ……………………(4分)
∴
两边同除以
，得
………………………(6分)
∴
是以
为首项，
为公差的等差数列
∴
∴
………………………………(8分)
(Ⅱ) ∵
∴
令
，则
……………………………(9分)
∵
∴
……………………(10分)
∴
∴
令
①
则
② …………………(12分)
①一②，得
∴
……………………………(14分)
练习册系列答案
阅读快车系列答案
相关题目
中，
，
，其前
项和
满足
，令
，求证：
．
，均存在
，使得
时，
．
中，
，且
．(Ⅰ) 求数列
，数列
的前
项和为
，试比较
与
的前
，求证：对任意
，都有 
．
中，
，且
． 
，数列
的前
项和为
，试比较
与
的前
．求证：对任意
，
．
中，
，
. (1)求
; (2)求
的前n项和,证明:
.
中，
.
的值（只写结果）并求出数列
，若对任意的正整数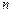
，当
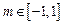时，不等式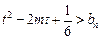
恒成立，求实数
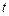的取值范围。