题目内容
11.数列{an}的首项a1=b(b≠0)的前n项和为Sn,数列{Sn}为等比数列,q为公比,且0<q<1,(1)求证:数列{an}以第二项起成等比数列;
(2)求:a1S1+a2S2+…+anSn.
分析 (1)运用等比数列的通项公式和数列的通项与求和之间的关系,即可得证;
(2)运用等比数列的求和公式,计算即可得到.
解答 (1)证明:数列{Sn}为等比数列,q为公比,且0<q<1,
即有Sn=S1•qn-1=a1•qn-1=b•qn-1,
n=1时,a1=S1=b,
n>1时,an=Sn-Sn-1=b•qn-1-b•qn-2=b(q-1)•qn-2,
对n=1不成立.
故数列{an}以第二项b(q-1),成公比为q的等比数列;
(2)解:a1S1+a2S2+…+anSn=b2+b2q(q-1)+b2q3(q-1)+…+b2(q-1)q2n-3
=b2+b2q(q-1)(1+q2+…+q2n-4)
=b2+b2q(q-1)•$\frac{1-{q}^{2n-2}}{1-{q}^{2}}$
=b2+b2q•$\frac{{q}^{2n-2}-1}{q+1}$.
点评 本题考查等比数列的通项和求和公式的运用,考查数列的通项和求和之间的关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
2.已知θ∈(0,$\frac{π}{2}$),p,q∈R,“p<q”是“(sinθ)p>(sinθ)q”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
11.已知cos(75°+α)=$\frac{1}{3}$,则sin(15°-α)值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | -$\frac{{2\sqrt{2}}}{3}$ |
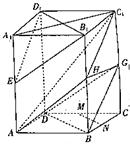 如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.
如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.