题目内容
（2011•丰台区二模）用max{a，b}表示a，b两个数中的最大数，设f（x）=max{-x2+8x-4，log2x}，若函数g（x）=f（x）-kx有2个零点，则k的取值范围是（ ）
分析：首先要从正面求解得到结论：有2个零点，即函数y=f（x）与直线y=kx有两个交点．然后从反面考虑，利用排除法．首先k=0不成立，排除D，其次，二次函数的顶点是（4，12），与原点连线的斜率是3，显然成立，排除A，B，得到结果．
解答：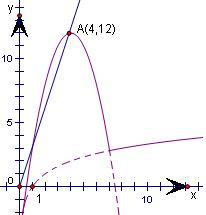
解：函数g（x）=f（x）-kx有2个零点，
即函数y=f（x）与直线y=kx有两个交点．如图，
然后从反面：排除法．
首先k=0不成立，排除D，
其次，二次函数的顶点是（4，12），与原点连线的斜率是3，显然成立，排除A，B，得到结果选C．
故选C．
解：函数g（x）=f（x）-kx有2个零点，即函数y=f（x）与直线y=kx有两个交点．如图，
然后从反面：排除法．
首先k=0不成立，排除D，
其次，二次函数的顶点是（4，12），与原点连线的斜率是3，显然成立，排除A，B，得到结果选C．
故选C．
点评：本小题主要考查学生对函数概念的理解、函数单调性的应用、根的存在性及根的个数判断等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
（2011•丰台区二模）如图所示，已知