Question

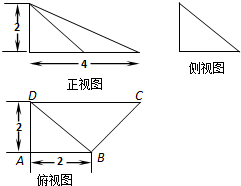
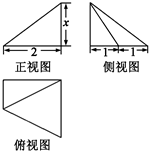
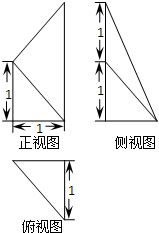
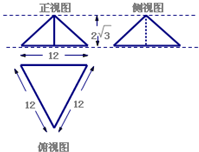
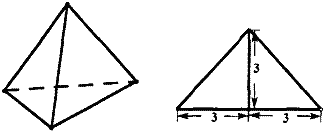
某空间几何体的三视图如图所示，则此几何体的体积（　　）

A．有最大值2

B．有最大值4

C．有最大值6

D．有最小值2

Answer 1

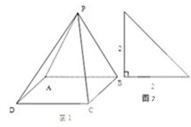
由三视图该几何可知：体是一个三棱锥，OA=OC=x，PO⊥底面ABC，PO=3，AB=BC=2，OB=y．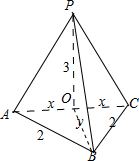
∴x²+y²=4，V_{三棱锥P-ABC}=

1

3

×

1

2

×2xy×3=xy≤

x2+y2

2

=

4

2

=2，当且仅当x=y=

2

时取等号．
故此几何体的体积有最大值2．
故选A．