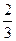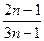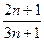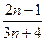题目内容
(12分)数列{an}满足a1=1,a2=2,an+2=(1+cos2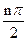 )an+sin
)an+sin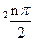 ,n=1.2.3…
,n=1.2.3…
(1)求a3.a4并求数列{an}的通项公式
(2)设bn=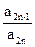 ,令 Sn=
,令 Sn=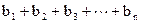 ,求 Sn
,求 Sn
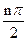 )an+sin
)an+sin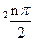 ,n=1.2.3…
,n=1.2.3…(1)求a3.a4并求数列{an}的通项公式
(2)设bn=
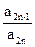 ,令 Sn=
,令 Sn=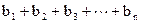 ,求 Sn
,求 Sn(1)an=
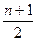
(2)Sn=2-
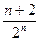
解:(1)a3="2 " a4="4 "
当n=2k-1时,a2k+1 =a2k-1+1
=a2k-1+1
∴a1,a3,a5…a2k-1…成等差数列,公差d=1
 a2k-1=1+(k-1)·1=k
a2k-1=1+(k-1)·1=k
∴an=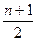
当n=2k时 a2k+2=2·a2k
即数列a2,a4,a6…成等比数列,公比q=2
a2k=2·2k-1=2
∴an=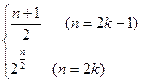
(2)bn=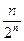
Sn=1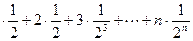
由错位相减得:
Sn=2-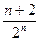
当n=2k-1时,a2k+1
 =a2k-1+1
=a2k-1+1∴a1,a3,a5…a2k-1…成等差数列,公差d=1
 a2k-1=1+(k-1)·1=k
a2k-1=1+(k-1)·1=k∴an=
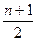
当n=2k时 a2k+2=2·a2k
即数列a2,a4,a6…成等比数列,公比q=2
a2k=2·2k-1=2
∴an=
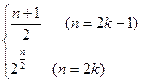
(2)bn=
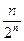
Sn=1
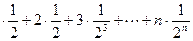
由错位相减得:
Sn=2-
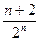

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
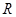 上的函数
上的函数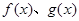 满足
满足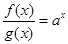 ,
,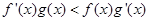 ,
, 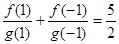 ,有穷数列
,有穷数列 (
(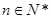 )的前
)的前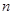 项和等于
项和等于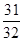 , 则n等于
, 则n等于 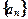 为一等差数列,其中
为一等差数列,其中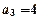 ,
,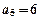 ,
,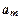
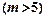 ,使得
,使得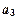 、
、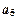 、
、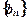 满足
满足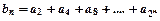 ,求
,求 的公差为
的公差为 ,且
,且 ,若
,若 ,则
,则 为
为 



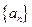 为等差数列,
为等差数列,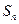 为其前
为其前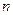 项和,且
项和,且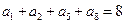 ,则
,则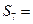


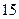

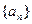 中,若
中,若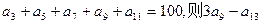 的值为( )
的值为( )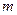 名,编号为
名,编号为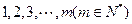 ,该校共开设了
,该校共开设了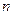 门选修课,编号为
门选修课,编号为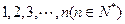 .定义记号
.定义记号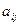 :若第
:若第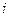 号学生选修了第
号学生选修了第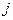 号课程,则
号课程,则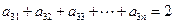 ,则该等式说明的实际含义是3号同学选修了 ▲ 门课程
,则该等式说明的实际含义是3号同学选修了 ▲ 门课程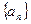 中,
中,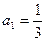 ,且对任意
,且对任意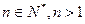 都有
都有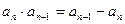 成立,令
成立,令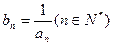 (1)求数列
(1)求数列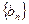 的通项公式;(2)求数列
的通项公式;(2)求数列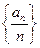 的前n项和
的前n项和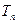 。
。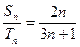 ,则
,则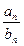 等于( )
等于( )