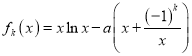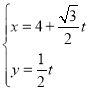题目内容
【题目】已知函数![]() 图像上的点
图像上的点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若函数![]() 在
在![]() 时有极值,求
时有极值,求![]() 的表达式;
的表达式;
(2)函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)对函数![]() 求导,由题意点
求导,由题意点![]() 处的切线方程为
处的切线方程为![]() ,可得
,可得![]() ,再根据
,再根据![]() ,又由
,又由![]() 联立方程求出
联立方程求出![]() 的值,从而求出
的值,从而求出![]() 的解析式.(2)由题意得函数
的解析式.(2)由题意得函数![]() 在区间
在区间![]() 上单调递增,对其求导可得
上单调递增,对其求导可得![]() 再区间
再区间![]() 上大于或等于
上大于或等于![]() ,从而求解
,从而求解![]() 的取值范围.
的取值范围.
试题解析:由题意得![]() ,
,
因为函数![]() 在
在![]() 处的切线斜率为-3,
处的切线斜率为-3,
所以![]() ,
,
又![]() 得
得![]() .
.
(1)函数f(x)在![]() 时有极值,所以
时有极值,所以![]()
解得![]() ,b=4,c=-3
,b=4,c=-3
所以![]() .
.
(2)因为函数f(x)在区间[-2,0]上单调递增,所以导函数![]() 在区间[-2,0]上的值恒大于或等于零,
在区间[-2,0]上的值恒大于或等于零,
则,得![]() ,
,
所以实数b的取值范围为[4+∞)

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】10月1日,某品牌的两款最新手机(记为![]() 型号,
型号,![]() 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日当天,从![]() ,
,![]() 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用![]() 表示其中
表示其中![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,![]() 型号手机的销售成本
型号手机的销售成本![]() (百元)与销量(部)满足关系
(百元)与销量(部)满足关系![]() .若表中
.若表中![]() 型号手机销量的方差
型号手机销量的方差![]() ,试给出表中5个手机店的
,试给出表中5个手机店的![]() 型号手机销售成本的方差
型号手机销售成本的方差![]() 的值.(用
的值.(用![]() 表示,结论不要求证明)
表示,结论不要求证明)