题目内容
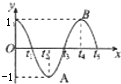 已知函数y=sin(ωx+?)(ω>0,-
已知函数y=sin(ωx+?)(ω>0,-| π |
| 2 |
| 5 |
分析:由函数的图象可得函数为偶函数,结合?的范围求得?=
,设函数的周期为T,由|AB|=
=
,解得T的值,
再由T=2=
求得ω 的值.
| π |
| 2 |
4+(
|
| 5 |
再由T=2=
| 2π |
| ω |
解答:解: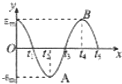 ∵函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,∴?=
∵函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,∴?=
,
∵A,B两点间距离为
,设函数的周期为T,
则由|AB|=
=
,解得T=2,即
=2,ω=π.
故 y=sin(πx+
).
故选B.
 ∵函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,∴?=
∵函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,∴?=| π |
| 2 |
∵A,B两点间距离为
| 5 |
则由|AB|=
4+(
|
| 5 |
| 2π |
| ω |
故 y=sin(πx+
| π |
| 2 |
故选B.
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,余弦函数的对称性,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知函数y=|sin(2x-
)|,则以下说法正确的是( )
| π |
| 6 |
A、周期为
| ||||
B、函数图象的一条对称轴是直线x=
| ||||
C、函数在[
| ||||
| D、函数是偶函数 |

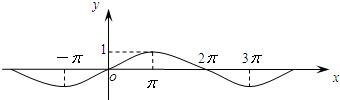 已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象所有点向右平移
已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象所有点向右平移