题目内容
16.已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N•)在函数y=2x2+x-1的图象上,则数列{an}通项公式为an=$\left\{\begin{array}{l}{2,n=1}\\{4n-1,n≥2}\end{array}\right.$.分析 点(n,Sn)(n∈N•)在函数y=2x2+x-1的图象上,可得Sn=2n2+n-1.当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1.
解答 解:∵点(n,Sn)(n∈N•)在函数y=2x2+x-1的图象上,
∴Sn=2n2+n-1,
当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2+n-1-[2(n-1)2+(n-1)-1]=4n-1,
∴an=$\left\{\begin{array}{l}{2,n=1}\\{4n-1,n≥2}\end{array}\right.$.
故答案为:an=$\left\{\begin{array}{l}{2,n=1}\\{4n-1,n≥2}\end{array}\right.$.
点评 本题考查了递推关系的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知双曲线的中心在原点,焦点在x轴上,若其渐进线与圆x2+y2-6y+3=0相切,则此双曲线的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{6}$ |
7.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )
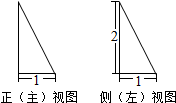

| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
4.“实系数一元二次方程x2+x+c=0有虚根”是“c>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.