题目内容
16.已知f(x)=cos2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$,g(x)图象由f(x)向右平移$\frac{π}{12}$个单位,横坐标伸长到原来的两倍,纵坐标缩为原来的m(0<m<$\frac{1}{2}$).向上平移一个单位得到.(1)求f(x)最小正周期和递减区间;
(2)求g(x)的表达式;
(3)判断g(x)=x实根个数.
分析 (1)由和差角公式化简可得f(x)=sin(2x+$\frac{π}{6}$),易得最小正周期和递减区间;
(2)由图象变换的规则,逐步变换可得;
(3)作出函数y=x和g(x)的图象,数形结合可得.
解答 解:(1)化简可得f(x)=cos2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$•2sinxcosx+$\frac{1}{2}$(2cos2x-1)
=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x
=sin(2x+$\frac{π}{6}$),
∴f(x)最小正周期T=$\frac{2π}{2}$=π,
由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$可解得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
∴函数f(x)的递减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z);
(2)由图象变换可得y=sin(2x+$\frac{π}{6}$)向右平移$\frac{π}{12}$个单位得到y=sin[2(x-$\frac{π}{12}$)+$\frac{π}{6}$]=sin2x,
再横坐标伸长到原来的两倍得到y=sinx,然后纵坐标缩为原来的m倍得到y=msinx,
再向上平移一个单位得到g(x)=msinx+1;
(3)作出函数y=x和g(x)=msinx+1,(0<m<$\frac{1}{2}$)的图象,
可得g(x)=x实根个数为1
点评 本题考查两角和与差的三角函数公式,涉及三角函数的周期性和单调性以及图象变换,属中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6.已知椭圆的左焦点为F1,右焦点为F2.若椭圆上存在一点P,满足线段PF2相切于以椭圆的短轴为直径的圆,切点为线段PF2的中点,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
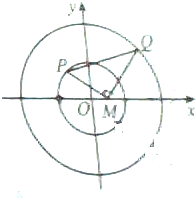 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.