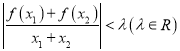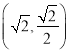题目内容
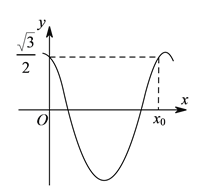
【题目】函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)写出![]() 及图中
及图中![]() 的值.
的值.
(Ⅱ)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(Ⅰ)![]() ,
, ![]() .(Ⅱ)最大值
.(Ⅱ)最大值![]() ,最小值
,最小值![]() .
.
【解析】试题分析:(1)将点 代入,由已给条件可求得
代入,由已给条件可求得![]() ;由
;由![]() 并结合图象可求得
并结合图象可求得![]() .
.
(2)由(1)可得到![]() ,由
,由![]() ,得
,得![]() ,可得在
,可得在![]() 和
和![]() 时,函数
时,函数![]() 分别取得最大值和最小值。
分别取得最大值和最小值。
试题解析:(Ⅰ)∵图象过点 ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
, ![]() ,
,
又![]() 的周期为
的周期为![]() ,结合图象知
,结合图象知![]() ,∴
,∴![]() .
.
(Ⅱ)由题意可得![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取得最小值
取得最小值![]() .
.
点睛: 三角函数式的化简要遵循“三看”原则
(1)一看“角”,这是最重要的一环,通过看角之间的区别和联系,把角进行合理的拆分,从而正确使用公式;
(2)而看“函数名称”看函数名称之间的差异,从而确定使用公式,常见的有“切化弦”;
(3)三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,如“遇到分式通分”等.

练习册系列答案
相关题目
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(I)若花店一天购进![]() 枝玫瑰花,写出当天的利润
枝玫瑰花,写出当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(II)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各需求量的频率作为各需求量发生的概率.
天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望.
的分布列,数学期望.
(ii)若花店计划一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?只写结论.
枝?只写结论.