题目内容
16.已知函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=x2(1)求f(0)
(2)求f($\frac{2015}{2}$)
(3)画y=f(x)草图
(4)求y=f(x)与y=log5x图象的交点个数.
分析 (1)直接代值计算即可,
(2)先根据函数y=f(x)(x∈R)满足f(x-1)=f(x+1),得出f(x)是周期为2的周期性函数,而f($\frac{2015}{2}$)=f(504×2-$\frac{1}{2}$)=f(-$\frac{1}{2}$),问题得以解决.
(3)根据函数的周期性画出图形即可
(4)再把函数的零点转化为两函数图象的交点,利用图象直接得结论.
解答 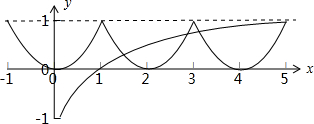 解:(1)∵x∈[-1,1]时,f(x)=x2,
解:(1)∵x∈[-1,1]时,f(x)=x2,
∴f(0)=0,
(2)∵函数y=f(x)(x∈R)满足f(x-1)=f(x+1),
∴f(x+2)=f(x),f(x)是周期为2的周期性函数,
∴f($\frac{2015}{2}$)=f(504×2-$\frac{1}{2}$)=f(-$\frac{1}{2}$)=$\frac{1}{4}$,
(3)根据函数的周期性画出图形,如图所示,
(4)再画出y=y=log5x图象,
由图可得y=f(x)与y=log5x的图象有4个交点.
点评 本题考查抽象函数图象和性质,关键是求出函数的周期为2,并结合函数的图象进行判断,属于中档题.

练习册系列答案
相关题目
6.8名学生和2位老师站成一排合影,2位老师恰好相邻的排法种数为( )
| A. | A${\;}_{9}^{9}$A${\;}_{2}^{2}$ | B. | A${\;}_{9}^{9}$ | C. | A${\;}_{10}^{10}$ | D. | 2A${\;}_{10}^{9}$ |